translated by damien from sildes of Sisi Ramanan

Unit 2 Lagrange Optimization - Adjustment Cost and Tobin’s Q

1. Optimization by lagrange Multiplier

Lagrange Multiplier

A useful formulation for constrained optimization is the concept of Lagrangean function. With the use of lagrangean multipliers, the Lagrangean incorporates all constraints in the objective function. Any constrained optimization becomes unconstrained. The multipliers also have an intuitive economic interpretation. A general constrained maximization problem can be written as:
  拉格朗日函数的概念是约束的优化的一个有用的公式。 利用拉格朗日乘数（乘子），拉格朗日函数将所有约束条件纳入目标函数。 任何有约束的优化都会变成无约束的。 这个乘子也有一个直观的经济学解释。 一般的约束最大化问题可以写成：
\[ max f(x) \] subject to some constraints:
  受某些限制：
\[ g_i(x) = c_i \, \text{ for } i = 1,…m \]

Here the function to be maximized \(f(x) \), called the objective function, is defined on a vector of decision variables:
  在这里，将要最大化的函数成为目标函数，定义在一个决策变量的向量上： \[ x = (x1, x2,…x_n)’ \]

Note: We could also have inequality constraints and m is usually less than n but not necessarily.
  注：我们也可以有不等式约束，m通常小于n，但不一定。

The Lagrangean function of this constrained maximization problem is written as:
  这个约束最大化问题的拉格朗日函数写为：

\[ \mathscr{L}(x, \lambda) = f(x)-\lambda_i(g_i(x) -c_i) \]  \( \lambda_i\)’s are called Lagrange multiplier.
  \( \lambda_i\)’s被叫做拉格朗日乘子。

The necessary condition for maximum is then given by the first order conditions:
  最大值的必要条件由一阶条件（FOC）给出：

\[ \frac{\partial \mathscr{L}(x, \lambda)}{\partial x_i} = 0 \ , \text{for} \ i = 1, …n \]

 and
  和

\[ \frac{\partial \mathscr{L}(x, \lambda)}{\partial x_i} = 0 \ , \text{for} \ i = 1, …m \]

If the objective function is concave and the constraints are convex and differentiable, then the necessary conditions are also suffcient for a maximum. All the models that we deal with in this course satisfy this criterion.
  如果目标函数是凹的，且约束是凸的和可微的，那么最大值的必要条件也是充分的。我们在本课程中处理的所有模型都满足这个标准。

The Lagrange multiplier can be interpreted as the rate of change in the maximal value of the objective function as the constraint is relaxed.
  拉格朗日乘子可以解释为目标函数的最大值随着约束的放松而变化的速率。

2. Adjustment Cost Model

This model assumes there are costs of quickly adjusting the capital stock. Adjustment costs can arise when new capital goods are installed, training workforce, learning by doing, shutting down plants. We will focus on convex adjustment costs. The model introduces a very useful concept, the Tobin’s Q.
  该模型假设存在快速调整资本存量的成本。当新的资产财货被安置，培训劳动力，边干边学，关闭工厂时，就产生调整成本。我们将关注为凸函数的调整成本。这个模型引入了一个非常有用的概念，托宾Q。

Adjustment Costs can be internal or external.
  调整成本可以是内部的或者外部的。

Internal adjustment costs arise when firms face direct costs of changing their capital stocks. Example: Installing new capital, training workforce to operate new machines etc.
  内部调整成本会在企业面临改变资本的直接成本时产生。例子：安置新资产，培训员工操作新机器等等。

External adjustment costs arise when the price of capital goods fluctuates depending on how much and how fast new capital is installed. Example: Any production that relies on external intermediaries to supply capital goods.
  外部调整成本在资本财货价格波动时产生，这取决于新资本的安装量和安装速度。例子：任何依赖外部中介机构提供资本资本货物的的生产。

We will focus on internal adjustment costs.
  我们将要关注内部调整成本。

The firm lives forever, time period is infinite.
  企业永存，时间无限。

The firm is assumed to maximize its value subject to an increasing and convex cost of adjusting capital. The value of the firm is the expected present discounted sum of dividends (or equivalently net profits). A constant interest rate is used for discounting time.
  假设企业在资本调整成本为凸函数且不断增加的情况下实现其价值最大化。公司的价值是股息（或相当于净利润）的预期现值折现总和。固定利率用于贴现时间。

The value of the firm at time t, Vt , is given by:
  公司在时间t时的价值，Vt，由以下公式得出： \[ V_t = E_t \left \lbrace \sum^\infty_{i=0} \left ( {1 \over 1+r} \right)^i D_{t+i} \right \rbrace
\tag{1} \label{firmValue} \]

We use the expectations operator \(E[.]\) since future dividends are essentially unknown (random variables).
  我们使用期望算子\(E[.]\) ，因为未来股息基本上是未知的（随机变量）。

The problem of the firm is to maximize this value, given that current investments become productive with one period delay, the capital accumulation equation is given by:
  公司的问题是使该价值最大化，鉴于当前投资在一个时期的延迟后才具有生产性，资本积累方程由以下公式得出：

\[ K_{t+1} = (1-\delta)K_t+I_t \tag{2} \label{capitalAccumulation} \]

Every unit of investments incurs quadratic adjustment cost \( AC_t \) of the form:
  每一个投资单位都会产生如下形式的二次调整成本：

\[ AC_t = \frac{\phi}{2} I^2_t \tag{3} \label{adjustmentCost} \]

 Note: When \( \phi = 0 \), we have no adjustment costs.
  注意：当\(\phi = 0 \)时，我们没有调整成本。

Dividends can be defined as profits net of investment expenditures and adjustment costs:
  股息可定义为扣除投资支出和调整成本后的利润：

\[ D_t = \pi (\theta_t, K_t) - I_t - AC_t \tag{4} \label{dividends}
\]

Here we have assumed that the price of capital is one.
Profits, \( \pi (\theta_t, K_t) \), is a function of capital at time \( t \) and also productivity, \(\theta_t\). The variable \(\theta_t\) measures the technological innovation in a firm. More innovative firms can produce more output at the same level of inputs. The time variation in this variable is usually modelled as a stochastic process (a sequence of random variables indexed with time).
  这里我们假设资本的价格是1。利润\( \pi (\theta_t, K_t) \)是时间资本\( t \)和生产率\(\theta_t\)的函数。变量\(\theta_t\)衡量企业的技术创新。更具创新性的企业可以在相同的投入水平上产出更多的产出。 这个变量的时间变化通常被建模为一个随机过程（一系列随时间变化的随机变量）。

So we can finally write the complete firm’s problem as follows:
  因此，我们最终可以将整个公司的问题写如下：

\[ max E_0 \sum^{\infty}_{t=0} \beta^t \left [ \pi (\theta_t, K_t) - I_t - \frac{\phi}{2} I^2_t
\right] \]

 subject to the capital accumulation constraint in equation \eqref{capitalAccumulation} each period. Here \( \beta = {1 \over 1+r}\) is the discount factor and \( {1 \over \beta} = 1+r \) is the discount rate.
  受方程 \eqref{capitalAccumulation}中每一期资本累积的约束，这是折现系数和折现率。

Note: This constraint should hold for every period \( t = 0, 1, 2,…\infty \).

The Lagrangean can be written as:
  拉格朗日函数可以被改写为：

\[\mathscr{L} = E_0 \sum^{\infty}_{t=0} \beta^t \left [ \pi(\theta_t, K)_t - I_t - \frac{\phi}{2} I^2_t - q_t( K _{t+1} - (1-\theta)K_t -I_t) \right ] \tag{5} \label{lagrange}\]

  where \(q_t \) is the lagrange multiplier.
  在这里 \(q_t \) 是拉格朗日乘子。

The First Order Conditions (FOC) for the Lagrangean are given by:
  拉格朗日函数的一阶条件（FOC）由以下公式给出：

\[ \frac{\partial \mathscr{L}}{\partial I_t} = 0 \implies q_t = 1 + \phi I_t \tag{6} \label{lagrangeFOC1} \]

\[ \frac{\partial \mathscr{L}}{\partial K_{t+1}} = 0 \implies q_t = E_t \beta [ \pi_K (\theta_{t+1} + K_{t+1} ) + q_{t+1} (1-\delta) ] \tag{7} \label{lagrangeFOC2} \]

 and
  和

\[ \frac{\partial \mathscr{L}}{\partial q_t} = 0 \implies K_{t+1} = (1-\delta) K_t + I_t \tag{8} \label{lagrangeFOC3}
\]

Combining the first two FOC’s, we have the condition for investment decision:
  结合前两个FOC的等式，我们便有了投资决策的条件：

\[{ \underbrace{ 1 + \phi I_t}_{ \text{Marginal Cost} } } = { \underbrace{E_t \beta [ \pi_K (\theta_{t+1} + K_{t+1} ) + q_{t+1} (1-\delta) ]}_{\text{Expected discounted Marginal Benefit}} } \tag{9} \label{combination}\]

The left hand side is marginal cost of an additional unit of capital, the price of capital (1) plus the marginal adjustment cost ( \( \phi I_t \) ). The right hand side is expected discounted value of marginal profitability and value of non-depreciated capital.
  左边是额外单位资本的边际成本，即资本价格（1）加上边际调整成本( \( \phi I_t \) )。右边是边际盈利能力的预期折现值和未折旧资本的价值。

The multiplier gives us the shadow value of capital. The shadow value describes how much the value of the firm will rise if we were to have an additional unit of capital. Equivalently, the marginal profit net of adjustment cost that we can generate from an additional unit of capital. The advantage of this model is that we have also defined the value of capital or the value of firm.
  乘数（乘子）给了我们资本的影子价值。 影子价值描述了如果我们增加一个单位的资本，公司的价值会上升多少。相当于，我们可以从额外的单位资本中产生的调整成本的边际利润。 该模型的优点是我们还定义了资本价值或企业价值。

3. Tobin’s Q

  托宾Q

Since the price of a new capital good is equal to one, the optimal investment rule says to keep investing in capital until the marginal value of this action given by \(q_t \) equals its cost.
  由于一种新的资本货物的价格等于1，最优投资规则规定继续投资于资本，直到这个行为的边际价值等于其成本为止。

\(q_t \) is called Marginal Q or Tobin’s Q, named after the economist James Tobin.
  \(q_t \)被称为边际q或托宾q，以经济学家詹姆斯·托宾的名字命名。

From the first order condition in eq. \eqref{lagrangeFOC1}, we have:
  根据等式.\eqref{lagrangeFOC1}中的一阶条件，我们得到：

\[ q_t = 1 + \phi I_t \]

 in terms of investments,
  至于投资， \[ I_t = {1 \over \phi} (q_t - 1) \tag{10} \label{investment} \]

This says that net investments will be positive if and only if \(q_t > 1 \). The parameter \(\phi \) governs how sensitive investment is to \(q_t \). This equation also says that a firms’ investment should only be a function of \(q_t \) and parameters.
  这意味着净投资只有当且仅当 \(q_t > 1 \) 时才是正的。参数 \(\phi \) 控制投资对 \(q_t \) 的敏感程度。这个等式还表明，一个公司的投资应该只是 \(q_t \)和参数的函数。

The investment rule clearly shows that investment depends on future expected profitability. Since capital is durable and capital boosts production and profits this makes sense.
  投资规则清楚地表明，投资取决于未来的预期盈利能力。既然资本是持久的，资本可以促进生产和利润，这是有道理的。

\(q_t \) or marginal Q is what we call in statistics a suffcient statistic for investment. That is, knowing Q is suffcient to understand all relevant information related to the investment decision, see eq. \eqref{investment}.
  \(q_t \) 或边际q是我们在统计学中称之为投资的“充分统计”。 也就是说，知道Q不足以理解与投资决策相关的所有信息，参见\eqref{investment} 等式。

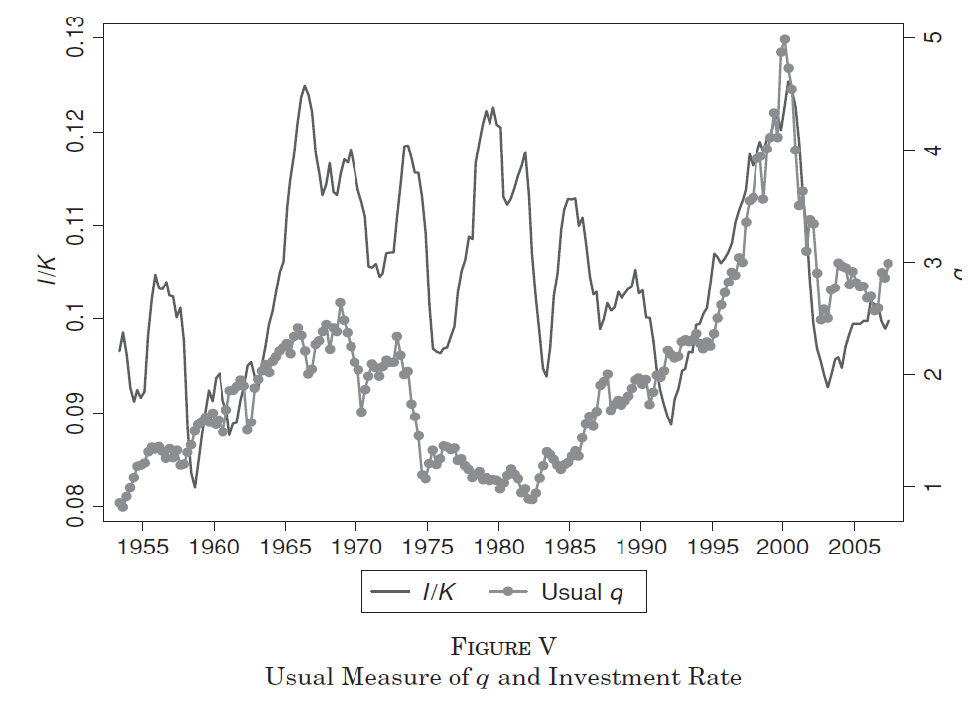
The assumption of convex adjustment costs implies that the investment will be smooth as firms cannot tolerate very large changes in their capital stock. This model thus, predicts that firms should continuously adjust their capital stock in response to changing conditions. In other words, investment should always be small and continuous. Unfortunately, this is not true in empirical data where investment is highly discontinuous and lumpy. This is the main limitation of the convex adjustment cost model.
  凸调整成本的假设意味着投资将是平稳的，因为企业不能容忍其资本存量的巨大变化。 因此，这个模型预测企业应该持续调整他们的资本存量以应对不断变化的环境。 换言之，投资应始终保持小规模和持续性。 不幸的是，这种不连续的、不连续的投资数据并不真实。 这是凸调整成本模型的主要局限性。

The value of the firm derived here is also a measure of its stock market value. The model then implies that rises in future expected profitability will raise its firm value (stock market value). It also predicts that investment is a positive function of future expected profits. Combining these two statements, we get the prediction that investment and the stock market will move together. Higher stock market valuation \( \implies\) higher investment.
  从这里得出的公司价值也是衡量其股票市场价值的一个指标。 然后，该模型暗示未来预期盈利能力的提高将提高其公司价值（股票市场价值）。 它还预测投资是未来预期利润的正函数。 结合这两种说法，我们得出了投资和股市将共同变动的预测。 股市估值越高 \( \implies\)投资就越高。

A historical example where this prediction is confirmed was during the technology boom of the 1990s in NASDAQ stock exchange. Both stock prices (firm value) and corporate investment surged together. We will have more on this relationship in a later lecture.
  这一预测得到证实的一个历史例子是，上世纪90年代纳斯达克证券交易所（NASDAQ stock exchange）的科技繁荣时期。 股票价格（公司价值）和企业投资一起飙升。 我们将在后面的讲座中详细介绍这种关系。

4. Further Reading:

Gregory Chow, Dynamic Economics: Optimization by the Lagrange Method. Chapter 1: 1.1-1.3 and 1.8.