translated by damien from Christian Ewald

Financial Markets, Securities & Derivatives - Unit 2 Forwards, Futures and Options

1. Introduction

• This unit starts by introducing the concept of forward contracts and futures contracts as well as options
• the mechanics of the futures markets are analysed using real-world examples
• then the unit demonstrates how to use arbitrage arguments to determine forward and futures prices of an investment asset from its spot price and other ovservable market variables
• next, the valuation of forward contracts is studied in rich detail
• the principles of hedging is understood using a numerical example
• then, the specifications of an option contract, the profits and payoffs of different option positioins are studied
• next, the put-call prity is derived and understood

• lastyly, examples of option trading strategites are introduced and analysed

• Suggested reading
  Hull, John (2015). Options, Futures and Other Derivatives, 9th edition, Pearson, Chapters 2, 3, 5 and 10-12

1.1 Forwards

Forward Contracts

1. Definition: A forward contract is an agreement, i.e. a binding commitment, to buy or sell an asset at a certain future time for a certain price.

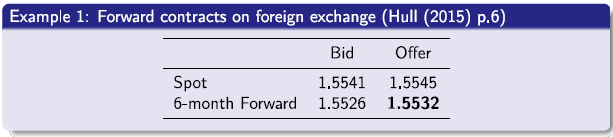
A forward contract is traded in the over-the-counter market. The party who takes the long position agrees to buy the underlying asset on a certain specified future date for a certain specified price. The other party who takes the short position agrees to sell the asset on the same date for the same price.

1.2 Futures

Futures Contracts

1. Definition: A futures contract is an agreement between two parties to buy or seAll an asset at a certain time in the future for a certain price with (daily) clearing through a margin account.

Unlike forward contracts, futures contracts are normally traded on an exchange. This suggests that, the exchange specifies certain standardized features of the contract, i.e. the underlying asset, the contract size and delivery details; the exchange also provides a mechanism that gives the two parties of the futures contract a guarantee that the contract will be honored.

• Underlying assets: commodities, e.g. lumber, crude oil, gold; financial assets, e.g. stock indices, currencies, Treasury bonds.

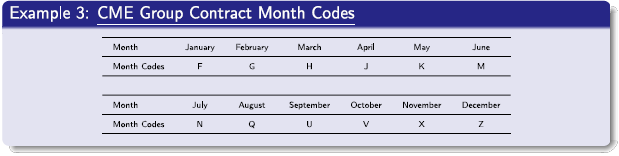
• Delivery Month: A futures contract is referred to by its delivery month. For instance, the product code of CME Gold futures contract for December 2019 is ‘GCZ19’.

The trader who agrees to buy has a long futures position in the contract; the trader who agrees to sell has a short futures position in the contract. The price agrred to is the current futures price, which is determined by the law of supply and demand.

• Market Quetos: last trade, change, priort settlement, open, high, low, trading volume.

1.3 The Operation of Margin Accounts

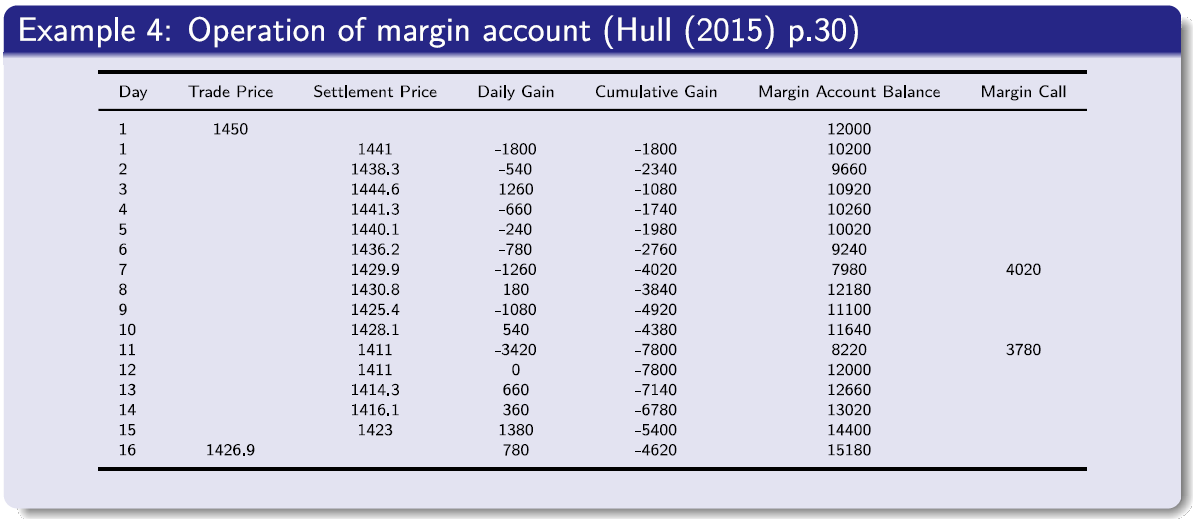
1. One of the key roles of the exchange is to use margin accounts to organize trading so that contract defaults are avoided.

2. The amount that must be deposited at the time the contract is entered into is known as the initial margin.

3. At the end of each trading day, the margin account is adjusted to reflect the investor’s gain or loss. This practice is referred to as daily settlement or marking to market. More specifically, a trade is first settled at the close of the day on which it takes place. It is then settled at the close of trading on each subsequent day. By contrast, the forward contracts are settled at the expiry.

4. To ensure that the balance in the margin account never becomes negative a maintenance margin is set. If the balance in the margin account falls below the maintenance margin, the investor receives a margin call and is expected to top up the margin account to the initial margin level by the end of the next day.

5. The extra funds deposited are known as a variation margin. If the investor does not provide the variation margin, the broker closes out the position by entering into the opposite trade to the original one.

An example

Both forward and futures contracts are agreements to buy or sell an assset for a certain price at a certain future time. The main differences between forward and futures contracts are summarised in the following table.

1.4 Arbitrage

Arbitrage: Non-dividend-paying Stock

• Arbitrage: an arbitrage is defined as a trading strategy that require zero initial investment, has zero probability of losing money, and has a positive probability of making money.

A mathematical model that admits arbitrage leads to contradictions. Wealth could be generated from nothing in such a model, in consequence prices would adjust through supply and demand to eliminate the arbitrage. CAPM uses a slightly different notion of arbitrage!

We use arbitrage arguments to determine the forward and futures prices of an investment asset from its spot price and other observable market variables.

1.5 Forward Price (no income)

Forward Price for an Investment: No Income

From Example 5, the first arbitrage works as long as the forward price is greater than 40.5; the second arbitrage works as long as the forward price is less than 40.5.

Based on the previous analysis, now consider a forward contract on an investment asset with price \( S_0\) that provides no income ( and no costs), e.g. non-dividend-paying stocks. The relationship between \( F_0\) and \( S_0\) is

If \( F_0 > S_0 e^{rT} \), arbitrageurs can buy the asset and short forward contracts on the asset; if \( F_0 < S_0 e^{rT} \), arbitrageurs can short the asset and enter into long forward contract on it.

Intuition: consider the following strategy: buy one unit of the asset and enter into a short forward contract to sell it for \( F_0\) at time \(T\). Buying the asset costs \( S_0\), the strategy is certain to lead to a cash inflow of \( F_0\) at time \(T\). Therefore, \( S_0\) must equal the present value of \( F_0\), i.e. \( S_0 = F_0 e^{-rT}\). Thus, \( F_0 = S_0 e^{rT}\).

Indeed, using equation \eqref{forwardPrice}, the forward price from Example 5 is \(F_0 = 40e^{0.05 \times 0.25} = 40.5.\)

Arbitrage: Coupon-bearing Bond

Guideline for arbitrage: the guiding principle of taking arbitrage opportunity is to buy low and sell high. In other words, when the forward price is higher than its no-arbitrage theoretical value, arbitrageurs buy the underlying asset; when the forward price is lower than its no-arbitrage theoretical value, arbitrageurs sell the underlying asset.

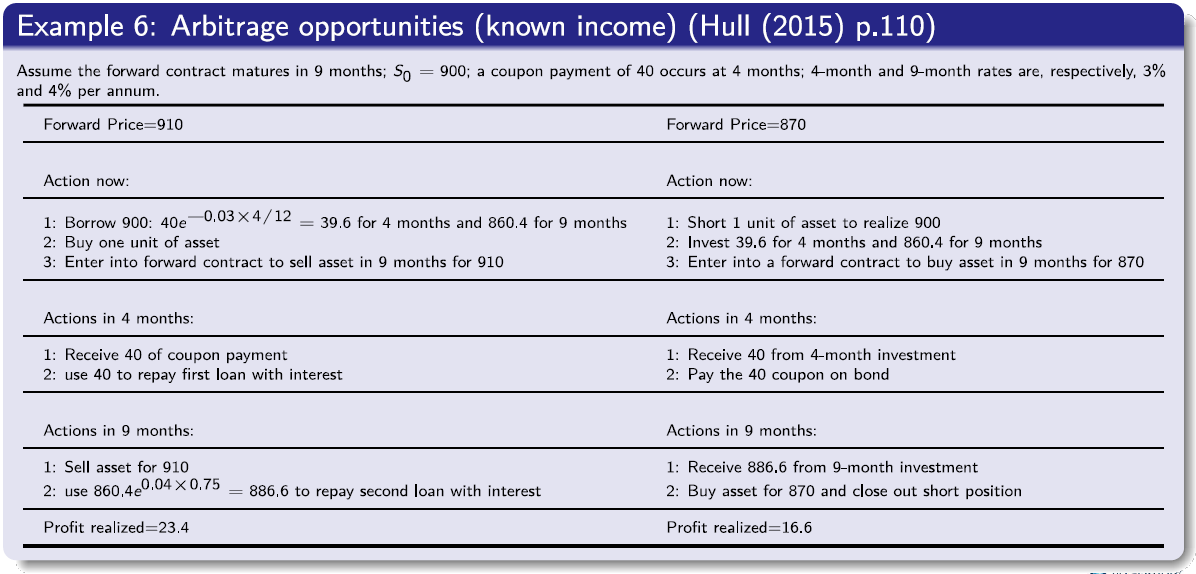
Forward Price for an Investment Asset: Known Income

When an investment asset will provide known income with a present value of \( G \) during the life of a forward contract, we have:

Indeed, in Example 6, the forward price is:

If \( F_0 > (S_0 - G) e^{rT}\), an arbitrageur can lock in a profit by buying the asset and shorting a forward contract on the asset; if\( F_0 < (S_0 - G) e^{rT}\), an arbitrageur can lock in a profit by shorting the asset and taking a long position in a forward contract.

We now consider the case where the asset underlying a forward contract provides a known yield, i.e. a return provided by an instrument. This means that the income is known when expressed as a percentage of the asset’s price at the time the income is paid.

The yield is normally measured with continuous compounding. A yield measured with one compounding frequency can be translated to a yield measured with another compounding frequency:

\[ R_c = m \cdot ln(1+ \frac{R_m}{m}) \tag{4} \label{yield} \]

 where \(R_c\) denotes the annualized continuous-compounding yield; \(m\) is the compounding frequency; \(R_m\) represents the annualized discrete-compounding yield.

After translating discrete-compounding yield into continuous-compounding yield, we are ready to derive the forward price. Define \( q \) as the average yield per annum on an asset during the life of a forward contract with continuous compounding. The forward price of an investment asset with known yield is:

\[ F_0 = S_0 e^{(r-q)T} \tag{5} \label{forwardPriceWithYield} \]

Consider a 6-month forward contract on an asset that is expected to provide income equal to	2% of the 
asset price once during a 6-month  period;  r = 10%; So =25. Therefore, the annualized yield is 4% with 
semiannual compounding. Using equation (4), the corresponding continuous-compounding yield can be 
computed as 3.96%. Thus, from equation (5), the forward price is

\[ 25e^{(0.1-0.0396) \times 0.5} = 25.77 \]

Valuing Forward Contracts

Timing of the life of forward contract:

Time 0 is the beginning of the life of the forward contract; time \(t\) is the current time, i.e. today; time \(T\) is the delivery date (or maturity) of the forward contract.

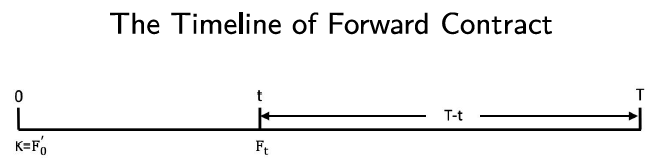
Suppose \(K\) is the delivery price for the contract that was negotiated at time 0 and \(K = F’_0 \), i.e. is set equal to the forward price at time 0. As time passes, \(K\) stays constant (because it is agreed at time 0). \( F_t\) is the forward price that would be applicable if we negotiated the contract today. \(T- t\) is the time to maturity. In addition, we define \(f_t\) as the value of forward contract today.

Because it costs nothing to enter into a forward contract, the value of a forward contract at the time it is first entered into is zero. As time evolves, due to the fluctuations of the interest rate and the spot price of underlying asset, the forward price \(f_t\) changes and the value of the contract can become either positive or negative.

A general result, applicable to the value of any long forward contract, is:

\[ f_t = (F_t - K)e ^{-r(T-t)} \tag{6} \label{forwardValue} \]

Intuition:

1. We form a portfolio today consisting of (a) a forward contract to buy the underlying asset for \( K\) at time \( T\) T, and (b) a forward contract to sell the asset for \(F_t\) at time \(T\).

2. The payoff from the portfolio at time \(T\) is \(S_T - K\) from contract (a) and \(F_t - S_T\) from contract (b).

3. The total payoff is \( F_t - K\) and is known for certain today. The portfolio is therefore a risk-free investment and its value today is the payoff at time \(T\) discounted at the risk-free rate, i.e. \( (F_t - K)e^{-r(T-t)}\).

4. The value of the forward contract (b) is worth zero because \(F_t\) is the forward price that applies to a forward contract entered into today.

5. Therefore, the value of a long forward contract to buy an asset for \( K\) at time \(T\) must be \( (F_t - K)e^{-r(T-t)}\).

6. Similarly, the value of a short forward contract to sell the asset for \( K\) at time \(T\) is \( (K- F_t)e^{-r(T-t)}\).

Are Forward Prices and Futures Prices Equal?

\( \underline{\text{Technical Note 24}} \) from Hull (2015) uses the arbitrage argument to show that, when the risk-free rate is constant, the forward price for a contract with a certain delivery date is in theory the same as the futures price for a contract with that delivery date. This argument can be extended to the case where the interest rate is a known function of time, i.e. as long as the interest rate is not stochastic.

The intuition is as follows: Assume spot and interest rate are positively correlated.

• if the interest rate rises, then the spot price is likely rising as well \(\implies \) due to the daily setllement in the futures contract, money can be released from the margin account and be invested at a higher interest rate
• if the interest rate falls, then the spot price is likely falling as well \(\implies \) due to the daily settlement, money needs to be paid into the margin account, but this money can now be borrowed at a lower interest rate
• relative to a forward contract, which is not affect by any of this, the futures contract benefits from interest rate movements, and this raises the futures price as compared to the forward price

If spot and interest rate are negatively correlated, the opposite effect occurs, which lowers the futures price relative to the forward price.

However, the theoretical differences between forward and futures prices for contracts that last only a few months are in most circumstances sufficiently small to be ignored. In Hull (2015), for most purposes it is reasonable to assume that forward and futures prices are the same.

Futures Prices of Stock Indices

A stock index can usually be regarded as the price of an investment asset that pays dividends. The investment asset is the portfolio of stocks composing the stock index, and the dividends paid by the investment asset are the dividends that would be received by the holder of this portfolio. It is usually assumed that the dividends provide a known yield (relative to the stock index) rather than a known cash income.

Assume \(q \) is the average annualised dividend yield during the life of the contract, the futures price, \( F_0 \) , is:

Index Arbitrage: if \(F_0 > S_0 e ^{(r-q)T} \), arbitrage profit can be made by buying the stocks underlying the index at the spot price and shorting the stock index futures contracts; on the other hand, \(F_0 < S_0 e ^{(r-q)T} \), profit can be obtained by shorting or selling the stocks underlying the stock index and taking a long position in futures contracts.

Hedging: Basic Principles

Many market participants in futures markets are hedgers. Their aim is to use futures markets to reduce exposure to a particular risk, e.g. fluctuation in the crude oil price. In other words, the hedgers take a position in futures contracts which neutralises the risk as far as possible.

• Consider a compony A that expects it will gain 10000 for each 1 cent increase in the price of crude oil over the next 3 months and lose 10000 for each 1 cent decrease in the price of crude oil during the next 3 months.
• To hedge, compony A should take a short futures position that is designed to offset th is risk. The futures position shouId lead to a loss of 10000 for each 1 cent increase in the price of crude oil over the 3 months, and a gain of 10000 for each 1 cent decrease in the price of crude oil during this period.
• In other words, if the price of crude oil goes down, the gain on the futures position offsets the loss; if the price of crude oil goes up, the loss on the futures position is offset by the gain from crude oil.

Short Hedges: a short hedge is a hedge that involves taking a short position in futures contracts.

• A short hedge is appropriate when the hedger already owns an asset and expects to sell it at some time in the future.
• A short hedge can also be used when an asset is not owned right now but will be owned at some time in the future.

Long Hedges: a long hedge is a hedge that involves taking a long position in futures contracts.

• A long hedge is appropriate when a company knows it will have to purchase a certain asset in the future and wants to lock in a price now.

Comment: if the exposure is such that the company gains when the price of the asset increases and loses when the price of the asset decreases, a short hedge is appropriate. On the other hand, if the exposure is such that the company gains when the price of the asset decreases and loses when the price of the asset increases, a long hedge is appropriate (Hull (2015)).

Cross Hedging

The asset underlying the futures contract is different from the asset whose price is being hedged. For example, an airline may want to hedge the fluctuation in the price of jet fuel. Because futures on jet fuel are not actively traded, the airline could use heating oil futures contracts to hedge its exposure to jet fuel price fluctuation.

Hedge Ratio: the ratio of the size of the position taken in futures contracts relative to the size of the exposure.

• When the asset underlying the futures contract is the same as the asset being hedged, i.e. no cross hedging, the hedge ratio is 1.
• When cross hedging occurs, the hedger needs to choose a value for the hedge ratio such that the variance of the value of the hedged position is minimised. This value of the hedge ratio is referred to as the minimum variance hedge ratio.

The Minimum Variance Hedge Ratio

Consider the case where the investor takes a long position in asset \(S\) and a short position in the futures contract \( F\). Define:

• \(\Delta S\): change in spot price during a period of time equal to the life of the hedge;
• \(\Delta F\): change in futures price during a period of time equal to the life of the hedge;
• \(\sigma _S\): standard deviation of \(\Delta S\);
• \(\sigma _F\): standard deviation of \(\Delta F\);
• \(\rho _{SF}\): correlation between \(\Delta S\) and \(\Delta F\);
• \(h\): minimum variance hedge ratio.

In addition, define \(\Delta U = \Delta S - h \Delta F\) as the hedged position.

To find the minimum variance hedge ratio \(h\), we need to minimise \(Var(\Delta U)\).

Using the definition of the hedged position, i.e. \(\Delta U = \Delta S - h \Delta F\) , we have:

 The Relationship between Variance of Hedged Position and Hedge Ratio (Hull (2015))

Therefore, by setting

we derive the value of the minimum variance hedge ratio:

The slope coefficient obtained from a linear regression of \(\Delta S\) on\(\Delta F\) (i.e. \(\Delta S _i = \alpha +\beta \Delta F _i \) ) is given by:

Therefore, from equation \eqref{minRatio} and \eqref{slopeCoefficient}, the hedge ratio is the slope coeffficient obtained from a linear regression of \(\Delta S\) against \(\Delta F\). This is relevant for empirical analysis.

Optimal Number of Contracts

Formula \eqref{minRatio} derived from \eqref{variance} covers the case, where one future contract covers one unit of the underlying, to hedge one unit of the asset. In general futures contracts cover a larger size in the underlying and are being used to hedge a larger size of the asset.
To calculate the number of contracts that should be used in hedging, define:

• \(N^*\): optimal number of futures contracts used for hedging;
• \(Q_A\): size of position being hedged; e.g. number of units of assets
• \(Q_F\): size of one futures contract; i.e the number of units of the underlying one future contract refers to

The futures contracts should be on \(hQ_A\) units of the asset. The number of futures contracts required is therefore given by

Using Stock Index Futures to Hedge Equity Portfolios

Stock index futures can be used to hedge equity portfolios. Define:

• \(V_A\): current value of the equity portfolio;
• \(V_F\) : current nominal value of one futures contract (i.e. the futures price times the contract size).

If the portfolio mirrors the index, i.e. \( \rho_{AF} =1\) and \( \sigma_A =\sigma _F\), the optimal hedge ratio \(h\) could be assumed to be 1. The number of futures contracts that should be shorted is:

• Suppose that a portfolio \(A\) worth 5050000 mirrors the S&P500 Index. The index futures price is 1010; each futures contract is on 250 times the index value.
• In this case, \(V_A = 5050000\); \(V_F = 1010 \times 250 = 252500\). Thus, \(N^* = 5050000 /252500 = 20\), i.e. 20 futures contracts need to be shorted to hedge the portfolio.

In the case that the portfolio does not mirror the stock index, we can use the beta from the CAPM to determine the number of futures contracts, i.e.

 where it is assumed that the maturity of the futures contract is close to the maturity of the hedge.

Intuition:

• By comparing equation \eqref{numbers} with equation \eqref{num2}, we see that \(\beta \) functions as \(h\).
  Because the hedge ratio \(h\) is the slope of the best-fit line from a linear regression of \(\Delta S\) against \(\Delta F\); \(\beta \) is the slope of the best-fit line when the return on the portfolio is regressed against the return on the stock index.
• suppose, for example, the portfolio’s \(\beta \) is 2, this portfolio is twice as sensitive to the movements in the stock index as a portfolio with a \(\beta \) of 1. It is therefore necessary to use twice as many futures contracts to hedge this portfolio.

Assume that a futures contract with time to maturity of 4 months is used to hedge the value of a portfolio over the next 3 months in the following situation:

In this case, \(V_F = 1010 \times 250 = 252500\). Using equation \eqref{num2}, the number of futures contracts that need to be shorted to hedge the portfolio is:

Now suppose the S&P 500 ndex turns out to be 900 in 3 months; and the futures price in 3 months is 902. The gain from the short position in the futures contract is:

The loss on the stock index is \(|(900 - 1000)/1000| = 10 \)%. The stock index pays a dividend of 1% per annum, or 0.25% per 3 months. Taking the dividends into account, the investor in the stock index would earn \(-10 \% + 0.25\% = -9.75\%\) over the 3-month period.

According to the CAPM, the expected return on the portfolio can be computed as:

The expected value of the portfolio at the end of the 3 months is therefore:

Thus, the expected value of the hedger’s position, i.e. the expected value of the portfolio plus the gain from the short futures position, is:

In Hull (2015), the (conditional) expected values of the hedger’s position are calculated for other values of stock index at maturity.The results are shown in the following table.

It can be seen from the table that the total value of the hedger’s position in 3 months is almost independent of the value of the index, i.e. the variance of the value of the hedged position has been minimised. In other words, the equity portfolio is hedged.

What is an Option Contract?

Types of Option: there are two types of option:

• Call Option: a call option gives the holder the right to buy the underlying asset by a certain date for a certain price;

• Put Option: a put option gives the holder the right to sell the underlying asset by a certain date for a certain price.

Option vs. Forward and Futures: it should be noted that an option gives the holder the right, but not the obligation, to buy or sell an asset. In other words, the holder does not have to exercise this right. This is what distinguishes options from forwards and futures, where the holder is obligated to buy or sell the underlying asset. Furthermore, whereas it costs nothing to enter into a forward or futures contract, there is a cost to acquiring an option.