Business
Life
about me
Damien

Mathematical Finance - Unit 0 Probability Review

金融数学（零）概率论回顾 2021/01/27

Unit 0 Probability Review

Uploaded by eva

Outline

1 Discrete Random Variables

1.1 Sample Space 样本空间

  • We collect the possible states of the world and denote the set by \( \Omega \). The states are called samples or elementary events.

  • The sample space \( \Omega \) is either countable or uncountable.
      我们收集世界的可能状态，并用Ω表示该状态。这些状态称为样本或基本事件。样本空间Ω是可数的或不可数的。

    • A toss of a coin: \( \Omega = \lbrace Head, Tail \rbrace = \lbrace H, T \rbrace. \)
    • The number of successes in a sequence of n identical and independent trials: \( \Omega = \lbrace 0, 1, . . . , n \rbrace \).
      n个相同且独立的试验序列中的成功次数：
    • The moment of occurrence of the first success in an infinite sequence of identical and independent trials: \( \Omega = \lbrace 1, 2. . . \rbrace \)
      相同且独立试验的连续序列中首次成功的时刻：
    • The lifetime of a light bulb: \( \Omega = \lbrace x \in R | x \geq 0 \rbrace \).
      一个灯泡的寿命：
  • The choice of a sample space is arbitrary and thus any set can be taken as a sample space. However, practical considerations justify the choice of the most convenient sample space for the problem at hand.
    Discrete (finite or infinite, but countable) sample spaces are easier to handle than general sample spaces.
      样本空间的选择是任意的，因此任何集合都可以作为样本空间。然而，出于实际考虑，我们需要为手头的问题选择最方便的样本空间。   离散（有限或无限，但可数）样本空间比一般样本空间更容易处理。

1.2 Discrete Random Variables

  • Examples of random variables: 随机变量示例
  • Prices of stocks. 股票价格
  • Exchange rates. 汇率
  • Payoffs corresponding to portfolios. 与投资组合相应的收益

"FIG.1"

定义（离散随机变量)
实值函数 X 的定义域 \\( \Omega \\) 值域实数R在一个离散样本空间 \\( \Omega = \omega _k\\) 中，其中 *I* 是可数的。这个X 称为离散随机变量。

"FIG.2"   定义(概率)
  映射P：定义域 \( \Omega \) 的取值在[0,1]之间，被称为离散样本空间\( \Omega \)上的概率。

1.3 Probability Measure

Let F = \( 2^\Omega \) stand for the class of all subsets of the sample space \( \Omega \).
  F 代表样本空间 Ω 的所有子集的个数。Ω 为元素个数。

The set \( 2^\Omega \) is called the power set of \( \Omega \).
  \( 2^\Omega \) 是\( 2^\Omega \)的幂集。

Note that the empty set \(\emptyset\) also belongs to any power set.
  空集属于任何幂集。
"FIG.3"

  一个映射P的定义域F的取值在[0,1]之间，称为在（\( \Omega \)，F）上的概率测度。

  • 对于任一序列Ai 真包含于F，i=1，2，… \(A_i \cap A_j =\emptyset\)

  • Any set A \(\in\) F is called an event.
      任何一组A \(\in\) F都称为事件。

  • For any A \(\in\) F the equality \( P(\Omega \setminus A) = 1 - P(A) \) holds.
      任何A \(\in\) F等式\( P(\Omega \setminus A) = 1 - P(A) \)成立。

1.4 Probability Measure on a Discrete Sample Space

  离散样本空间上的概率测度

  • Note a probability P :\(\Omega \mapsto \) [0, 1] on a discrete sample space \( \Omega \) uniquely specifies probabilities of all events \( A_k = \{\omega_k\} \).
      注意，离散样本空间\( \Omega \)上的概率P :\(\Omega \mapsto \)[0，1]唯一地指定了所有事件的概率\( A_k = \{\omega_k\} \).

  • It is common to write as
      通常写作:

\[P( \lbrace \omega _k \rbrace ) = P(\omega _k)=p _k\]
  • The theorem shows that any probability on a discrete sample space \( \Omega \) generates a unique probability measure on (\( \Omega,F)\).
      该定理表明，离散样本空间\(\Omega\)上的任何概率在 （\(\Omega,F\)）上产生唯一的概率测度。

"FIG.4"

  • The proof of the theorem presents no difficulties, since \( \Omega \) is assumed to be discrete.
      由于\(\Omega\)被假定为离散的，定理的证明没有什么困难。

1.5 Example: Coin Flipping

  • Let X be the number of “heads” appearing when a fair coin is tossed twice. We choose the sample space \( \Omega \) to be
      让X是一枚公平的硬币,被抛两次时出现的“头”数。我们选择样本空间\( \Omega \)
\[\Omega = \\{ 0, 1, 2 \\}\]

  where a number \(k \in \Omega \) represents the number of times “head” has occurred.
  其中数字\(k \in \Omega \)表示“头”出现的次数。

  • The probability measure P on \( \Omega \) is defined as
    \( \Omega \)上的概率测度 P 定义为
\[P(k)= \left \lbrace \begin{array}{l} \frac {1} {4},\ \text{if}\ k = 0,2, \\\\ \frac {1} {2},\ otherwise. \end{array} \right.\]

  • We recognise here the binomial distribution with n = 2 and p = 1/2. A single flip of a coin is a Bernoulli trial.
      我们在这里认识到n=2且p=1/2的二项分布。一枚硬币的一次抛投就是伯努利实验。

  • We now suppose that the coin is not a fair one.
      我们现在认为这枚硬币不公平。

  • Let the probability of “head”be p for some \(p \ne 1/2\) .
      让“头”的概率为\(p \ne 1/2\)

  • Then the probability measure P is given by
      然后概率测度P由下式给出

\(P(k)= \begin{cases} q^2, &\text{if}\ k = 0, \\\\ 2pq, &\text{if}\ k = 1, \\\\ p^2, &\text{if}\ k = 2. \end{cases}\)

  • where q := 1-p is the probability of “tail” appearing.
      其中q:=1-p是出现“尾”的概率.

  • We deal here with the binomial distribution with n = 2 and 0 < p < 1.
      这里我们讨论的是n=2，0<p<1的二项分布.

2 Expectation of a Random Variable

2.1 Expectation

"FIG.5"
  定义（期望）
  设X是离散样本空间\( \Omega \)上的随机变量，赋以概率测度P.
  X的期望值（期望值或平均值）定义为
  （公式）

  \(E_p\)称为概率P上的期望算子。

  • Note that the expectation of a random variable can be seen as the weighted average.
      注意，随机变量的期望值可以看作加权平均值。

  • Since it is impossible to know the exact event in the future, expectation could help one to make decisions.
      由于不可能知道未来的确切事件，期望可以帮助人们做出决定。

2.2 Expectation Operator

  期望算子

  • Any random variable defined on a finite set \( \Omega \) admits the expectation.
      在有限集\( \Omega \)上定义的任何随机变量都有期望值。

  • When the set\( \Omega \) is countable (but infinite), we say that X is P-integrable whenever \(E_P (|X|) = \sum _{\omega\in\Omega} |X(\omega)|P(\omega) <\infty\).
    Then the expectation \(E_p (X) \)is well defined (and finite).
      当集合\( \Omega \)可数（但无限）时，我们说 X 当\(E_P (|X|) = \sum _{\omega\in\Omega} |X(\omega)|P(\omega) <\infty\) 时是p-可积（加）的 。
      期望 \(E_p (X) \)被明确定义（并且是有限的）。

"FIG.6"

  设X和Y是两个P-可积随机变量，P是离散样本空间\( \Omega \)上的概率测度，那么对于所有\(\alpha , \beta\in R \)

  因此概率空间的期望（定义域为X，值域为实数）是P-可积空间X上的线性算子。

"FIG.7"
  期望算子的证明：
  (公式)

  因此随机变量aX+bY属于X。期望的线性可以很容易地从定义中推导出来：
  (公式)

  其中\(\alpha\)和\(\beta\)是任意实数。

2.3 Expectation: Coin Flipping

  • A fair coin is tossed three times. The player receives one dollar each time “head” appears and loses one dollar when “tail” occurs.
      一枚硬币掷三次。玩家每次出现“头”时得到一美元，出现“尾”时损失一美元。

  • Let the random variable X represent the player’s payoff.
      让随机变量X代表玩家的收益。

  • The sample space \( \Omega \) is dened as\( \{\Omega=0,1,2,3 \}\) where \(k \in \Omega \) represents the number of times “head” occurs.
      样本空间\( \Omega \)被定义为\( \{\Omega=0,1,2,3 \}\)，其中\(k \in \Omega \)表示“head”出现的次数。

  • The probability measure is given by
      概率测度由下式给出

\[P(k)= \begin{cases} \frac {1} {8}, &\text{if}\ k = 0,3, \\\\ \frac {3} {8}, &\text{if}\ k = 1,2. \end{cases}\]
  • This is the binomial distribution with n = 3 and p = 1\2 .
      这是二项分布，n=3，p=1\2。
  • The random variable X is defined as
      随机变量X定义为
\[X(k)= \begin{cases} -3, &\text{if}\ k = 0, \\\\ -1, &\text{if}\ k = 1, \\\\ 1, &\text{if}\ k = 2, \\\\ 3,&\text{if}\ k = 3. \end{cases}\]
  • Hence the player’s expected payoff equals
    因此，玩家的预期收益等于
\[E_P(X)=\sum_{k=0}^3 X(k)P(k)\] \[=\frac {-3} {8}+(\frac {-3} {8})+\frac {3} {8}+\frac {3} {8} = 0.\]

2.4 Expectation of a Function of a Random Variable

  随机变量函数的期望

  • Let X be a random variable and P be a probability measure on a discrete sample space \( \Omega \). We define Y = f (X) where \(f : R \to R\) is an arbitrary function.
      设X是一个随机变量，P是离散样本空间\( \Omega \)上的概率测度。我们定义Y=f（X），其中\(f : R \to R\) 是一个任意函数。

  • Then Y is also a random variable on the sample space \( \Omega \) endowed with the same probability measure P. Moreover,
      那么Y也是样本空间\( \Omega \)上具有相同概率测度P的随机变量。此外，

\[E_p(Y) = E_p(f(X)) = \sum_{\omega \in \Omega}f(X(w))P(w).\]
  • If a random variable X is deterministic then \(E_p(X) = X\)and \(E_p(f(X)) = f (X)\).
    如果一个随机变量X是确定性的，那么

3 Equivalence of Probability Measures

  概率测度的等价性

Let P and Q be two probability measures on a discrete sample space \( \Omega \).
  设P和Q是离散样本空间\( \Omega \)上的两个概率测度。

"FIG.8"

  定义（概率测度的等价性）
  我们说概率测度P和Q是等价的,我们记作P~Q，无论何时所有的\(\omega\in \Omega\).

The random variable L : \( \Omega \mapsto R_+\)given as
  随机变量L的定义域\(\Omega\)的取值范围为正实数，表示为

\[L(w) = \frac {Q(\omega)} {P(\omega)}\]

is called the Radon-Nikodym density of Q with respect to P. Note that
  这称为Q相对于P.的拉东-尼科迪姆定理。记作

\[E_Q (X) = \sum_{\omega \in \Omega} X(\omega) Q(\omega)= \sum_{\omega \in \Omega} X(\omega) L(\omega) P(\omega) = E_P (LX)\]

3.1 Example: Equivalent Probability Measures

例子：等效概率度量

  • The sample space \( \Omega \) is defined as \( \Omega = \{1, 2, 3, 4\}\)
      样本空间\( \Omega \)定义为\( \Omega = \{1, 2, 3, 4\}\)
  • Let the two probability measures P and Q be given by
      设两个概率测度 P 和 Q 为
\[(\frac {1}{8},\frac {3}{8},\frac {2}{8},\frac {2}{8}) \ and\ (\frac {4}{8},\frac {1}{8},\frac {2}{8},\frac {1}{8})\]

  • It is clear that P and Q are equivalent, that is, \(P \sim Q\).
      很明显，P和Q是等价的，即P~Q.

  • Moreover, the Radon-Nikodym density L of Q with respect to P can be represented as follows
      此外，Q相对于P.的拉东-尼科迪姆L可以表示为

\[(4,\frac {1}{3},1,\frac {1}{2})\]
  • Check that for any random variable \(X: E_Q (X) = E_p (LX)\) .
      检查任意随机变量

3.2 Risky Investments

  风险投资

  • When deciding whether to invest in a given portfolio, an agent may be concerned with the “risk” of his investment.
      在决定是否投资某一特定投资组合时，代理人可能会考虑其投资的“风险”。

"FIG.9"

  例：   考虑一位投资者，他有机会在以下两种选择中进行选择：
  投资者得到或损失1000美元的概率相等。这个随机收益用\(X_1\)表示。
  投资者收到或损失1000000美元的概率相等。我们把这个随机收益表示为\(X_2\)。
  因此，在这两种情况下，预期收益值等于\(E_p（X_1）=E_p（X_2）=0\)

  下面的问题出现了：哪个选项更好？

4 Variance of a Random Variable

  随机变量的方差

4.1 Variance of a Random Variable

"FIG.10"
  离散样本集\( \Omega \)上随机变量 X 的方差为（公式）
  其中 P 是\( \Omega \)上的概率测度

  • Variance is a measure of the spread of a random variable about its mean and also a measure of uncertainty.
      方差是衡量随机变量均值分布的方法，也是不确定性的方法。

  • In financial applications, it is common to identify variance of the price of a security with its degree of “risk”.
      在金融应用中，通常会根据证券的“风险”程度来确定证券价格的差异。

  • Note that \(Var (X) = \sigma^2 \geq 0\) . It equals 0 if and only if X is deterministic.
      它等于0当且仅当X是确定的。

"FIG.11"

例子：

  • 期权1的方差等于（公式）

  • 期权2的方差等于（公式）

  • 因此，\(X_2\)表示的期权比\(X_1\)表示的期权风险更大。

  • 一个规避风险的代理人宁愿选择第一种而不是第二种。

  • 然而，一个喜欢冒险的代理人更喜欢第二种选择而不是第一种。

"FIG.12"

  定理（1.2）

  设X为随机变量，P为离散样本空间\( \Omega \)上的概率测度，则下列等式成立

  linearity（线性）

4.2 Independence of a Random Variable

  随机变量的独立性

"FIG.13"

  定义（独立性）
  两个离散随机变量X和Y称为独立的当且仅当对于所有\(X,Y \in R\)
  （公式）
  其中\(P（X=x）\)是事件\(\{X=x\}\)的概率

  独立随机变量X和Y的一个有用性质是 （公式）

  定理（1.3）
  设X和Y是两个独立的离散随机变量。对于任意的 \(\alpha,\beta \in R\)，
  （公式）

"FIG.14"

5 Continuous Random Variables

"FIG.15"

  定义（连续随机变量）

  如果存在实值函数f，则称样本空间\(\omega\)上的随机变量X具有连续分布
  （公式）
  那么\(f:R \to R_+\)称为连续随机变量X的概率密度函数（pdf)

Assume that X is a continuous random variable.
  假设X是一个连续的随机变量。

  • Note that a probability density function need not satisfy the constraint \(f (x) \le 1\).
      注意概率密度函数不需要满足约束
  • A function F (x) is called a *continuous random variable(cdf)
      函数F（x）称为连续随机变量
\[F (x) = P(X \le x) =\int_{-\infty}^x f(y)dy\]

The relationship between the pdf f and cdf F
  概率密度函数与连续随机变量的关系

\[F (x) =f (y )dy , f (x) =\int_{-\infty}^x f(y)dy \Leftrightarrow f(x)= \frac {d}{dx} F(x)\]
  • The expectation and variance of a continuous random variable X are defined as follows:
      连续随机变量X的期望和方差定义如下：

"FIG.16"
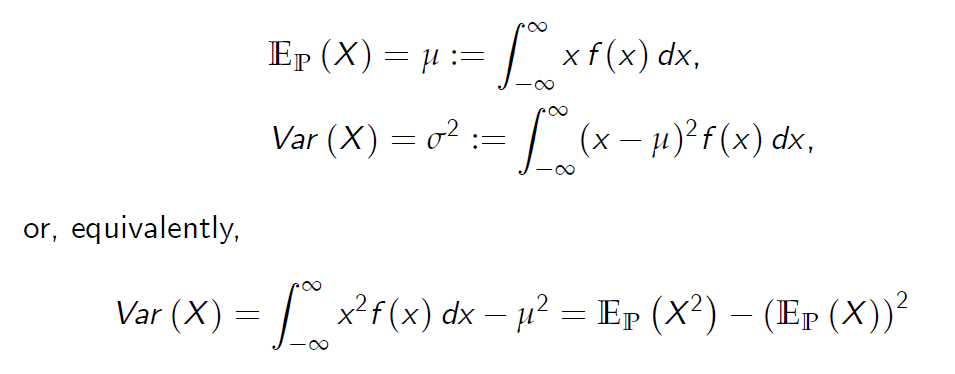
  or, equivalently,或者，等价地

  • The properties of expectations of discrete random variables carry over to continuous random variables, with probability measures being replaced by pdfs and sums by integrals.
      离散型随机变量的期望性质可以推广到连续型随机变量，概率测度可以用偏微分函数代替，和可以用积分代替。

6 Examples of Probability Distributions

  概率测度的示例

6.1 Discrete Probability Distributions

  离散概率分布

"FIG.17"
  例子

  • 设\(\Omega=\{0，1，2，…,n\} \)是样本空间，X是n个独立试验的成功次数，p是单个伯努利试验的成功概率。

  • 概率测度P称为二项分布，如果

"FIG.18"

  例子

  • 设样本空间为\(\Omega=\{0,1,2,…\}\)

  • 我们取一个任意数\(\lambda>0\)。

  • 概率测度P称为泊松分布，如果

  • 已知当n趋于无穷大且序列\(np_n\)趋于\(\lambda>0\)时，泊松分布可作为二项分布的极限。

"FIG.19"

  例子

  • 设\(\Omega=\{0,1,2,3…\}\)为样本空间，X为首次成功的独立试验次数。

  • 让p代表单一次试验成功的概率。

  • 概率测度P称为几何分布，如果

6.2 Continuous Probability Distributions

  连续概率分布

"FIG.20"

  • 如果X的概率密度函数等于(公式)，则X在区间（a，b）上具有均匀分布

"FIG.21"

  • 我们假设X在\(（0，\infty）\)上具有指数分布，如果其概率密度函数等于(公式)，则参数\(\lambda>0\)

"FIG.22"

  • 如果其pdf等于(公式)，我们说X具有高斯（正态）分布，平均\(μ\in r\)，方差\(\sigma^2>0\)

"FIG.23"

  • 如果我们设置μ=0和(\sigma^2=1\)，那么我们得到标准正态分布N（0，1）和以下pdf

  • 概率分布N（0，1）的cdf等于

  • N（x）的值可在累积标准正态分布表（也称为Z表）中找到。

6.3 LLN and CLT

"FIG.24"

  定理（大数定律）

  • 假设X1，X2 是独立且均值为μ的均匀分布的随机变量。然后以概率一

  定理（中心极限定理)

  • 假设X1，X2是独立且均布的随机变量，均值μ，方差\(\sigma^2>0\)。然后对于所有实数x

7 Correlation of Random Variables

  随机变量的相关性

7.1 Covariance of Random Variables

  随机变量的协方差

  • In the real world, agents can invest in several securities and typically would like to benefit from diversification.
      在现实世界中，代理商可以投资几种证券，通常希望从多元化中受益。

  • The price of one security may a¤ect the prices of other assets. For example, the stock index falling may lead the price of gold to rise.
      一种证券的价格可能会影响其他资产的价格。 例如，股指下跌可能导致金价上涨。

  • To quantify this effect, it is convenient to introduce the notion of covariance.
      为了量化此效果，可以方便地引入“协方差”的概念。

"FIG.25"

  两个随机变量X1和X2的协方差定义为

7.2 Correlated and Uncorrelated Random Variables

  相关和不相关的随机变量

  • The covariance of two random variables is a measure of the degree of variation of one variable with respect to the other.
      两个随机变量的协方差是一个变量相对于另一个变量的变化程度的度量。

  • Unlike the variance of a random variable, covariance of two random variables may take negative values.
      与随机变量的方差不同，两个随机变量的协方差可以取负值。

    • \(\sigma_{12} > 0 \): An increase in one variable tends to coincide with an increase in the other.
        一个变量的增加往往与另一个变量的增加一致。
    • \(\sigma_{12} < 0 \) : An increase in one variable tends to coincide with a decrease in the other.
        一个变量的增加往往与另一个变量的减少一致。
    • \(\sigma_{12} = 0 \): Then the random variables X1 and X2 are said to be uncorrelated. If \(\sigma_{12} \neq 0 \) then X1 and X2 are correlated.
        \(\sigma_{12} = 0 \)随机变量X1和X2不相关,\(\sigma_{12} \neq 0 \)则X1和X2相关。

"FIG.26"

7.3 Properties of the Covariance

  协方差的性质

"FIG.27"

  定理（1.4）
  以下属性有效：

  • 如果X1和X2是独立的，则它们是不相关的。

  • 相反，事实并非如此：X1和X2可能不相关，但它们不是独立的。

7.4 Correlation Coefficient

  相关系数

  • We can normalise the covariance measure. We obtain in this way the so-called correlation coefficient.
    我们可以将协方差度量标准化。 我们以此方式获得所谓的相关系数。

  • Note that the correlation coefficient is only defined when \(\sigma_1>0\) and \(\sigma_2>0\), that is, none of the two random variables is deterministic.
    请注意，仅当 \(\sigma_1>0\) and \(\sigma_2>0\)时才定义相关系数，也就是说，两个随机变量都不是确定性的。

"FIG.28"
定义（相关系数）
假设\(X_1\)和\(X_2\)是方差为\(\sigma_{1}^2\)和\(\sigma_{2}^2\),协方差为\(\sigma_{12}\)的两个随机变量。 相关系数为

7.5 Properties of Correlation Coefficient

  相关系数的性质

"FIG.29"

  定理
  相关系数满足\(-1 \leq \rho \leq 1\)。只要\(\rho\) = 0，随机变量\(X_1\)和\(X_2\)就不相关。
  证明
  结果来自于Cauchy-Schwarz不等式的应用:

  • \(\rho= 1\): If one variable increases, the other will also increase.
      如果一个变量增加，另一个变量也将增加。
  • \(0 < \rho< 1\): If one increases, the other will tend to increase.
      如果一个增加，则另一个趋向于增加。
  • \(\rho= 0\): The two random variables are uncorrelated.
      两个随机变量不相关。
  • \(-1 < \rho< 0\): If one increases, the other will tend to decrease.
      如果一个增加，则另一个趋于减少。
  • \(\rho= -1\): If one increases, the other will decrease.
      如果一个增加，另一个将减少。

7.6 Linear Regression in Basic Statistics

  基础统计学中的线性回归

  • If we observe the time series of prices of two securities the following question arises: how are they related to each other?
      如果我们观察两种证券价格的时间序列，就会产生以下问题：它们之间的关系如何？
  • Consider two random variables X and Y on the sample space \( \Omega = \{\omega_1,\omega_2, . . . ,\omega_n\}\). Denote \(X(\omega_i) = x_i \ and \ Y (\omega_i ) = y_i\).
      考虑样本空间\( \Omega = \{\omega_1,\omega_2, . . . ,\omega_n\}\)。。表示 \(X(\omega_i) = x_i \ and \ Y (\omega_i ) = y_i\)。
  • A linear fit is a relation of the following form, for \(\alpha, \beta \in R \),
      线性拟合是下列形式的关系，例如
\[y_i = \alpha+ \beta x_i + \epsilon_i .\]
  • The number \(\epsilon_i\) is called the residual of the ith observation.
      数字\(\epsilon_i\)称为第i次观测的残差。
  • In Statistics, the best linear fit to observed data is obtained through the method of least-squares: minimise \(\sum_{i=1}^n =1\epsilon_{i}^2\). The line \( y = \alpha+ \beta x\) is called the least-squares linear regression.
      在统计学中，观测数据的最佳线性拟合是通过最小二乘法得到的：最小化\(\sum_{i=1}^n =1\epsilon_{i}^2\)。 \( y = \alpha+ \beta x\)称为最小二乘线性回归。
  • We denote by \(\epsilon\) the random variable such that \(\epsilon(\omega_i)=\epsilon_i\) . This means that we set \(\epsilon := Y -\alpha+ \beta x\).
      我们用 \(\epsilon\)表示随机变量，\(\epsilon(\omega_i)=\epsilon_i\)。这意味着我们记作\(\epsilon := Y -\alpha+ \beta x\)。

7.7 Linear Regression in Probability Theory

  概率论中的线性回归

  • In Probability Theory, if \(\alpha\) and \(\beta\) are chosen to minimise
      在概率论中，如果选择\(\alpha\)和\(\beta\)以最小化
\[E_p \\{(Y-\alpha-\beta X)^2 \\}= E_p(\epsilon^2)=\sum_{i=1}^n \epsilon^2 (\omega_i) P(\omega_i)\]
then the random variable \(L _{Y X} := \alpha + \beta X\) is called the linear regression of Y on X.
  然后将随机变量\(L _{Y X} := \alpha + \beta X\)称为X上Y的线性回归。
  • The next result is valid for both discrete and continuous random variables.
    下一个结果对离散和连续随机变量均有效。

"FIG.30"

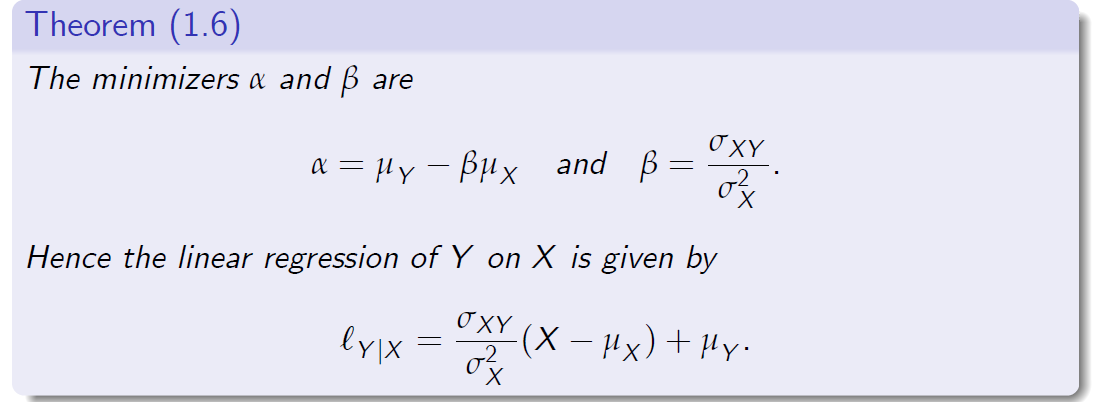
  Hebce 因此

7.8 Covariance Matrix

Recall that the covariance of random variables \(X_i\) and \(X_j\) equals
  回想一下，随机变量\(X_i\) and \(X_j\)的协方差等于
\(Cov(X_i,X_j)=\sigma_{ij} : E_p \{(X_i-μ_i)(X_j-μ_j)\}\)

where \(μ_i = E_P (X_i )\) and \(μ_j = E_P (X_j)\).

"FIG.31"

  定义（协方差矩阵）
  我们考虑随机变量\(X_i,i=1，2，…,n\)且方差\(\sigma_{i}^2=\sigma_{ii}\)且协方差\(\sigma_{ij}\) 。由此给出的矩阵 S 为:

"FIG.32"

  • S and P are symmetric and positive-definite matrices.
      S和P是对称的正定矩阵。

  • S = DPD where \(D^2\) is a diagonal matrix whose main diagonal coincides with the main diagonal in S.
      S=DPD，其中\(D^2\)是一个对角线矩阵，其主对角线与 S 中的主对角线重合。

  • If \(X_is\) are independent (or uncorrelated) random variables then S is a diagonal matrix and P = I is the identity matrix.
      如果\(X_is\)是独立（或不相关）的随机变量，那么s是对角矩阵，P=i是单位矩阵。

7.9 Linear Combinations of Random Variables

  随机变量的线性组合

"FIG.33"

  假设随机变量\(Y_1\)和\(Y_2\)是\(X_i\)的一些线性组合，即j=1，2存在向量\(a^j \in R^n\) 使得：（公式）
  inner product 内积

8 Conditional Distributions and Expectations

  条件分布和期望

For two random variables \(X_1\) and \(X_2\) and an arbitrary set A such that \(P(X_2 \in A) \neq 0\), we define the conditional probability 条件概率。

\[P(X_1 \in A_1 | X_2 \in A_2) := \frac {P(X_1 \in A_1,X_2 \in A_2)}{P(X_2 \in A_2)}\]

and the conditional expectation 条件期望

\[E_P(X _1 | X _2 \in A) := \frac {E_P(X_1 1_{X_2 \in A})}{P(X_2 \in A)}\]

where \(1_{\{X_2 \in A\} }: \Omega \to \{0,1\}\) is the indicator function 指示函数of \(\{X_2 \in A \}\), that is,

\[1_{X_2 \in A} (\omega)= \begin{cases} 1, &\text{if}\ X_2 (\omega)\in A, \\\\ 0, &\text otherwise. \end{cases}\]

8.1 Discrete Case

  离散情况

  • Assume that X and Y are discrete random variables
    假设X和Y是离散的随机变量
\[p_i = P(X = x_i ) > 0 for i = 1, 2, . . . and \sum_{i=1}^\infty p_i=1,\] \[\widehat{p_j}= P(Y = y_j ) > 0 for j = 1, 2, . . . and \sum_{i=1}^\infty \widehat{p_j}=1.\]

"FIG.34"
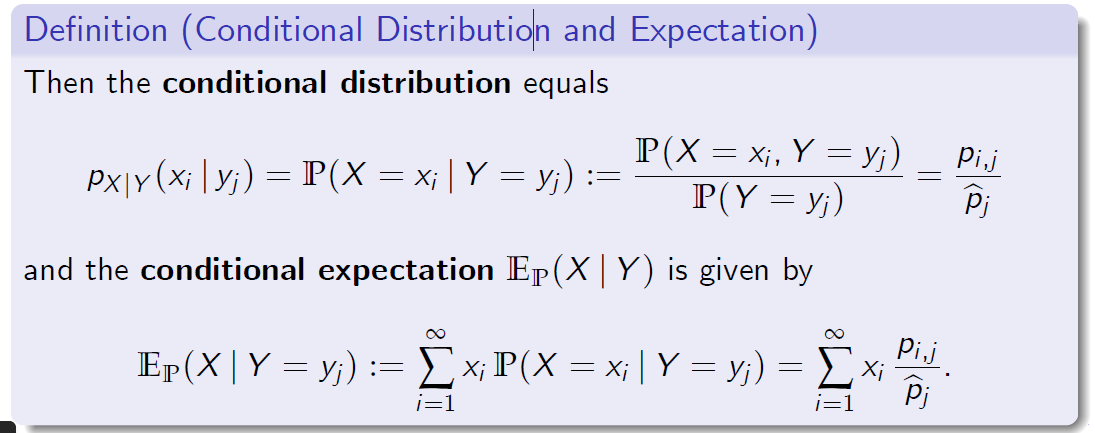
  定义（条件分布和期望)

  那么条件分布等于(公式)

  条件期望 \( E _P ( X | Y ) \) 由下式给出（公式）

"FIG.35"

8.2 Continuous Case

  连续案例

  • Assume that the continuous random variables X and Y have the joint pdf fX ,Y (x, y ).
      假设连续随机变量X和Y有关

"FIG.36"

  定义（条件pdf和cdf)

  给定明确的X，Y的条件pdf\(f_X（x）> 0\)等于

  给定X,Y的条件cdf等于

"FIG.37"

  连续案例
  定义（有条件的期望）   对所有x定义给定X的Y的条件期望，使得

  • An important property of conditional expectation is that
      条件期望的重要属性是
\[E_P(Y) = E_P(E_P(Y | X)) = \\int_{-\infty}^\infty E_P(Y | X = x)f_X (x) dx.\]
  • Hence the expected value \(E _P(Y)\) can be determined by first conditioning on X in order to compute \(E_P( Y | X )\) and then integrating with respect to the pdf of X.
      因此，可以通过首先对X进行条件化来确定期望值\(E _P(Y)\)以便计算 \(E _P( Y | X )\)），然后相对于X的pdf进行积分。

Show Disqus Comments

Post Directory