Unit 2 Elementary Market Model

Uploaded by eva

General approach in these lectures

• We want to learn how to price financial derivatives, say European Call Option. (Indeed, why not to start with something simple?)
    我们想学习如何对金融衍生产品定价，叫欧洲看涨期权。（实际上，为什么不从简单的事情开始？）

• Financial derivatives are written on the price of ‘underlying asset’: if its price satisfies certain condition at certain time we exercise So we need to do two things
    金融衍生产品是以“标的资产”的价格为基础的：如果它的价格在某一时间满足一定的条件，我们就要做两件事

  • Describe the price process of the underlying asset. Also, we may need to say something about other existing assets - i.e. describe the market.
      描述标的资产的定价过程。此外，我们可能需要讨论一些关于其他现有资产，即描述市场。

  • Specify the contract we want to price (derivative)
      指定我们要定价的合同（衍生产品）

• Then we need to price the derivative. Our approach to pricing will be based on arbitrage considerations.
    然后我们需要给衍生品定价。我们的定价方法将基于套利考虑。

• So in these lectures we will discuss, step by step, what is the fair price (so no arbitrage possible) and how to compute it.
    因此，在这些讲座中，我们将一步一步地讨论什么是公平价格（因此不可能套利）以及如何计算它。

Single Period Market Models

  单期市场模型

• Only one period is considered.
    只考虑一个周期。
  • The beginning of the period is usually set as t = 0.
      周期的开始通常设置为t=0
  • The end of the period is usually set as t = 1 (or T = 1).
      周期结束通常设置为t=1（或t=1）
• At t = 0, the prices of all assets are known and the investor can choose the investment.
    当t=0时，所有资产的价格都是已知的，投资者可以选择投资
• At t = 1, the prices of all assets are observed and the investor obtains a payoff corresponding to the current portfolio value.
    在t=1时，观察所有资产的价格，投资者获得与当前投资组合价值相对应的收益。
• Single period market models are not realistic, but allow us to illustrate important economic principles without su¤ering from (or enjoying) sophisticated mathematics.
    单周期市场模型并不现实，但它允许我们在不依赖（或享受）复杂数学的情况下阐明重要的经济原理。
• Single period market models are the atoms of the modern Mathematical Finance. A full understanding of their features (also drawbacks) is thus necessary for further developments.
    单期市场模型是现代数学金融的原子。因此，充分了解它们的特点（也有缺点）是进一步开发的必要条件。

Elementary Market Model: Informal Explanation

  初级市场模型：非正式解释

• Two points in time (one period)
    两个时间点（一个周期）

• Two assets: the underlying asset and the riskless asset (bank account with known rate of return)
    两种资产：标的资产和无风险资产（收益率已知的银行账户）

  • The riskless asset must always exist in these models - we need a benchmark. We always compare to what would happen if we invested everything into the riskless asset.
      这些模型中必须始终存在无风险资产——我们需要一个基准。我们总是比较如果我们把所有的东西都投资到无风险资产上会发生什么。

• Two states of nature: the price of underlying asset can only go up or down with given probability
    两种自然状态：标的资产的价格只有在给定的概率下才能上升或下降。

• The derivative security will be the European Call option: we will compute the fair price at time t = 0 of a contract to buy the underlying asset at time t = 1 and pay particular price K for a share.
    衍生证券将成为欧式看涨期权：我们将计算 t=0 时的公平价格，在 t=1 时购买标的资产，并以特定价格K购买股票

• Let’s start with all formal definitions   让我们从所有正式定义开始

Elementary Market Model

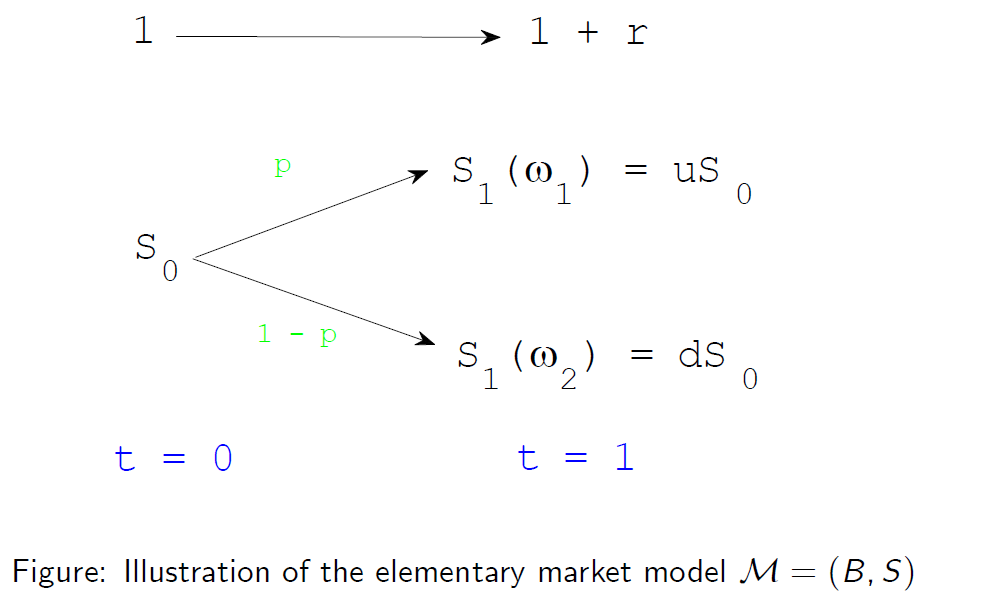
  基本市场模型的图示 M =（B，S）

• The investor has initial wealth x at t = 0 and is allowed to invest in a riskless asset B (bank account) and a risky asset S (stock). He purchases \(\phi\) shares of the stock and invest the remaining funds in his bank account (or borrows cash).
    投资者在 t = 0 时拥有初始财富 x ，并被允许投资无风险资产 B（银行账户）和风险资产 S（股票）。他购买了\(\phi\) 股股票，并将剩余的资金投资到他的银行帐户中（或借入现金）。

• Notation:
    表示法
  • Sample space 样本空间 : \(\Omega = \{\omega_1 , \omega_2\}\).
  • Probability measure 概率测度 : \(P(\omega_1) = p > 0 \) and \(P(\omega_2) = 1-p > 0\).
  • A deterministic interest rate 确定性利率 ：\(r > -1\).
  • The price of a risky asset at time t is denoted by 在时间t处风险资产的价格表示为：\(S_t\) .
  • We assume that 我们假设 \(S_0 > 0\) and we set 并设置 \(u = \frac {S_1 (\omega 1 )}{S_0}\) and \(d = \frac {S_1 (\omega_2)} {S_0}\)
  • M= (B, S) will be used to denote the model 将表示模型 。
• We suppose that 我们假设 0 < d < u, so that there are two distinct values of the future stock price 因此期货股票有两个不同的值 : \(S_1(\omega_1) > S_1(\omega_2)\).
• We do not assume that d < 1 or u > 1 (although d stands for ‘down’and u stands for ‘up’).
    我们不假设 d <1或 u> 1（尽管d代表’down’，而u代表’up’）

Why the Elementary Market Model?

  为什么要建立基本市场模型？

• Stock price movements are more complicated than indicated by the elementary market model. Hence it cannot be claimed that the elementary model gives a realistic picture of the stock price fluctuations.
    股票价格的变动比基本市场模型所表明的更为复杂。因此，不能说基本模型给出了股价波动的真实情况。

• Nevertheless, even in this simplistic framework the random character of the stock price is already visible and thus the problem of options pricing is non-trivial.
    尽管如此，即使在这种简单化的框架中，股票价格的随机性已经是可见的，因此期权定价的问题也不是小事。

• There are two important reasons why we consider this model:
    我们考虑此模型的两个重要原因：

  • First, the concept of arbitrage-free pricing of derivative securities can be clearly explained.
      首先，可以清楚地解释衍生证券的无套利定价概念。
  • Second, the binomial asset pricing model can be seen as an extension of elementary market models.
      其次，二项式资产定价模型可以看作是基本市场模型的扩展。

Outline

We will examine the following issues :
  我们将研究以下问题 :
1.Trading Strategies and Arbitrage-Free Models
  交易策略和无套利模型
2.Replication of Contingent Claims
  或有索取权的重复
3.Risk-Neutral Probability Measure
  风险中性概率测度
4.Put-Call Parity Relationship
  买卖权平价关系
5.Summary of the Elementary Market Model
  基本市场模型概述
6.Generalisation of the Elementary Market Model
  基本市场模型的推广

1.Trading Strategies and Arbitrage-Free Models

  交易策略和无套利模型

1.1 Trading Strategy and Wealth Process

  交易策略与财富过程

• For arbitrary real numbers x and \(\phi\), where x is the initial endowment and \(\phi\) is the number of shares of stock purchased or sold, the pair (x, \(\phi\)) is called the trading strategy.
    对于任意实数x和\(\phi\)，其中x是初始财富，\(\phi\)是买入或卖出的股票数量，这对(x, \(\phi\))称为策略交易。

• The initial value (or wealth) equals
    初始值（或财富）等于

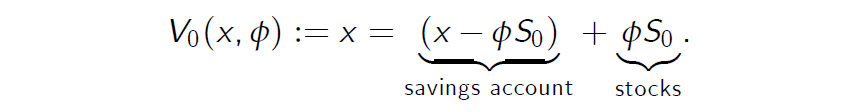
• For any trading strategy \((x, \phi)\), the investor obtains at time 1 the random payoff \(V_1(x, \phi)\), which equals for i = 1, 2
    对于任何策略交易\((x, \phi)\)，投资者在时间1获得随机收益\(V_1(x, \phi)\)，等于i=1，2

  定义（财富过程）
  策略交易\((x, \phi)\)的财富过程由\(（V_0(x, \phi)\)，\((x, \phi)\)）给出，其中\(V_0 (x, \phi)）=x \) and \(V_1((x, \phi)\)是随机变量.

1.2 Arbitrage

  套利 An essential feature of an efficient market is that for any trading strategy which can turn nothing into something, the investor who adopts it must also face the risk of loss.
  一个有效市场的一个基本特征是，对于任何一种不能把任何东西变成某种东西的策略交易，采用这种策略的投资者也必须面临损失的风险。 The following definition is thus a crucial step in the arbitrage pricing methodology.
  因此，以下定义是套利定价方法的关键步骤。

  单期市场模型中的交易策略\((x, \phi)\)称为套利机会，如果
  A1 即不需要初始投资
  A2 即没有赔钱的风险
  A3 即严格正的预期收益

1.3 Arbitrage-Free Model

  无套利模型 Note that, under A.2., the condition A.3. is equivalent to A.3’. There exists an \(w_i\) such that \(V_1(x, \phi)(\omega_i ) > 0 \).

  注意，在A.2.下，条件A.3.相当于A.3’。存在这样一个\(w_i\)使得\(V_1(x, \phi)(\omega_i ) > 0 \)。

  定义（无套利模型）
  如果模型中不存在套利机会，则称单期市场模型是无套利的

• Real markets sometimes exhibit arbitrage, but it is necessarily lasts for a very short time. The forces of supply and demand take actions to remove it as soon as someone discovers it.
    真实市场有时表现出套利行为，但这种行为必须持续很短的时间。一旦有人发现它，供求力量就会采取行动将其清除。
• A market model which admits arbitrage cannot be used for our purposes.
    允许套利的市场模型不能用于我们的套利机会。

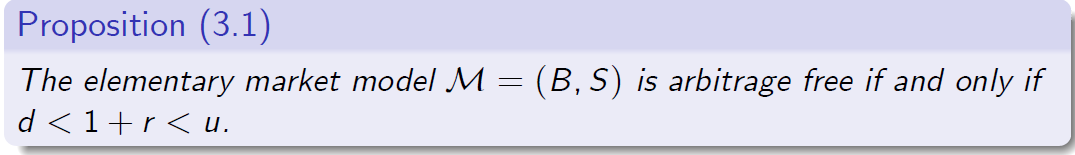
  基本市场模型M =（B，S）仅当且仅当没有套利时

1.4 Proof.

  证明 [Proof of Proposition 命题证明 3.1 (\(\Rightarrow)\)] To prove the ‘only if’part, we argue by contradiction:
  为了证明“仅当”部分，我们通过矛盾进行争论：

Assume first that \(d \ge 1 + r\) : 首先假设

• At t = 0, the investor borrows the amount \(S_0\) of cash on the money market and buys one share of the stock.
    在t = 0时，投资者在货币市场上借入现金\(S_0\)并购买一股股票。

• At t = 1, the investor sells the stock and thus receives either \(uS_0\) or \(dS_0\). He also pays back \((1 + r )S_0 \).
    在t = 1时，投资者卖出股票，因此收到\(uS_0\) or \(dS_0\)。 他还偿还\((1 + r )S_0 \)。
  Let us now assume that \(u \le 1 + r\) :
    现在让我们假设\(u \le 1 + r\)

• At t = 0, the investor borrows one share of the stock from the stock market and sells it immediately. He then invests \(S_0\) in the money market.
    在t = 0时，投资者从股票市场借入一股股票并立即出售。 然后，他将\(S_0\)投资于货币市场。

• At t = 1, the investor obtains \((1 + r )S_0\) from the bank account. He spends either \(uS_0\) or \(dS_0\) to buy one share of the stock and returns it to the original owner.
    在t = 1时，投资者从银行帐户中获得\((1 + r )S_0\)。 他花费\(uS_0\) or \(dS_0\)来购买一股股票，并将其退还给原始所有者。

• This completes the proof of the ‘only if’part.
    这样就完成了“仅当”部分的证明。

1.5 European Options

  欧洲期权

Definition (European Call and Put Options)
  定义（欧洲看涨和看跌期权）
A European call (put) option is a contract which gives the buyer the right to buy (sell) an asset at a future time T for a price K. The underlying asset, the maturity time T and the strike price K are specified in the contract.
  欧洲看涨（看跌）期权是赋予买方以价格K在未来时间T购买（出售）资产的权利的合约。标的资产，到期时间T和行使价K在合同中指定.

• How to compute the ‘fair price’ of a European call (put) option?
    如何计算欧式看涨（看跌）期权的“公平价格”？
• Payoff of European call option:
    欧洲看涨期权的收益
  • If the stock price \(S_1\) at T = 1 is above K then the holder obtains the payoff \(S_1 - K > 0\) from exercising the contract.
      如果在T = 1时股票价格\(S_1\)高于K(执行价格)，则持有者获得通过执行合同获得\(S_1 - K > 0\)。
  • If the stock price \(S_1\) at T = 1 is below K then the holder does not exercise the contract and this leads to the null payoff.
      如果在T = 1时股票价格\(S_1\) 低于K，则持有人不行使合同，这将导致零收益。
  • Hence the payo¤ of a European call option at time T = 1 is
      因此，在时间T = 1时，欧洲看涨期权的收益为
  \[\\\\ C_T= h(S_1)=max \{ 0,S_1-K \} =({S_1-K})^+\]
• Payoff of European put option:
    欧洲看跌期权的收益：
  • If the stock price \(S_1\) at T = 1 is above K then the holder does not exercise the contract; hence the payoff equals 0.
      如果在T = 1时股票价格\(S_1\)高于K，则持有人不行使合约；因此回报等于0。
  • If the stock price \(S_1\) at T = 1 is below K then the holder exercises the option and obtains the payoff \(K - S_1 > 0\).
      如果在T = 1时股价\(S_1\)低于K，则持有人行使期权并获得收益\(K - S_1 > 0\) - Hence the payoff of a European put option at time T = 1 equals
      因此，在时间T = 1时，欧洲看跌期权的收益等于

\[\\\\ P_T= h(S_1)=max \{ 0,K-S_1 \}=({K-S_1})^+\]

• European calls and puts are examples of contingent claims. Their payoffs \(C_T\) and \(P_T\) at expiry date T are random, but they only depend on the stock price \(S_1\) and strike K.
    欧洲看涨和看跌期权是或有债权的例子。他们在到期日T的收益\(C_T\) and \(P_T\)是随机的，但是它们仅取决于股价\(S_1\)并执行K。

We will now address the following general question:
  现在，我们将解决以下一般性问题：

• How to select an initial investment, x, and a trading strategy, \((x, \phi)\),in order to obtain the same wealth \(V_1(x, \phi)\) at time 1 as the payoff of a given contingent claim \(X = h(S_1)\)?
    如何选择初始投资x和交易策略\((x, \phi)\)，以便同时获得相同的财富\(V_1(x, \phi)\) 1是给定或有债权(或有索取权)的收益\(X = h(S_1)\)？

1.6 Example

• \(S_0 = 25, K = 35, r = 0 \)
• two states of nature: ‘price up to 40’and ‘price down to 20’.
    两种自然状态：“价格最高40”和“价格最低20”
• Investor expects \(S_{1}^u= 40\) with \(p_u = 0.5\) and \(S_{1}^d=20\) with \(p_d = 0.5)
    投资者期望
• How much to pay for the call option?   购买看涨期权要付多少钱？
• The seller knows that at time 1 she needs \((S_1 - K)^+ = (S_1 - 35)^+\)
    卖方知道在时间1时她需要
• The idea is to make initial investment to generate this money to meet the claim
    办法是进行初期投资以产生这笔钱来满足声明要求
• She can create a portfolio \((x - \phi S_0)\)into saving account and \((\phi S_0)\) into shares
    她可以创建投资组合\((x - \phi S_0)\)到保存帐户，并将\((\phi S_0)\)放入股票
• She will get 她会得到 \( (x - \phi S_0) (1 + 0) + 40 \phi \) or \((x - \phi S_0) (1 + 0) + 20 \phi \)
  • \((x -\phi S_0) (1 + 0) + 40 \phi = 5 \) then she can use these 5 + 35 from investor to deliver the share to the investor.
      然后，她可以用投资者提供的 5 + 35 把股份交付给投资者
  • \((x -\phi S_0) (1 + 0) + 20 \phi = 0 \) as the investor will not come
      因为投资者不会来

• So we need to solve the system of 2 equations with 2 unknowns
    所以我们需要求解有2个未知数的2个方程组

  • \((x - \phi S_0) (1 + 0) + 40 \phi = 5\)
  • \((x - \phi S_0) (1 + 0) + 20 \phi = 0 \)
• The solution (2 equations, 2 unknowns) at \((x - \phi S_0) = -5\) and \(\phi = \frac {1}{4}\).
  在\((x - \phi S_0) = -5\)处的解（2个方程式，2个未知数）和\(\phi = \frac {1}{4}\)

• The cost of building the portfolio at time zero
  在零时建立投资组合的成本 \((x -\phi S_0) + \phi S_0 = -5 + \frac {1}{4} * 25 =\frac {5}{4}=1.25\)

• So \(C_0 = 1.25\) is the price
  所以\(C_0 = 1.25\)是价格
• Subjective probabilities are irrelevant!
  主观概率是无关紧要的！
• Solving portfiolion is not always convinient, it is convenient to represent \(C_0\) as ‘expectation’of some payoff.
  求解投资组合并不总是方便的，可以方便地将\(C_0\)表示为收益的“期望”。
  • to define an expectation, we need to define appropriate probability measure.
    为了定义期望，我们需要定义适当的概率度量

2.Replication of Contingent Claims

  或有索取权（偶然债权）的重复

2.1 Replication of a Contingent Claim

基本市场模型 M =（B，S）中或有索取权 \(X = h（S_1）\)的复制策略（或套期保值）\(（x，\phi）\)是满足\(V_1（x，\phi）= h(S_1)\)的策略交易，即

以下定义符合一价定律
定义（套利价格） 假设基本市场模型 \(\cal M\) 是无套利的。如果\(（x，\phi）\)是或有索取权的复制策略，则 x 称为 t = 0 时的套利价格（或价格）。我们表示 \(x = \pi_0 (X)\)

2.2 Hedging of a Contingent Claim

或有索取权的对冲 Computation of the hedge and (unique) arbitrage price x of a contingent claim X = h(S1):
或有债权的对冲和（唯一）套利价格x的计算 X = h（S1）：

• By subtracting (2) from (1), we find the hedge ratio
  通过从（1）中减去（2），我们得出对冲比率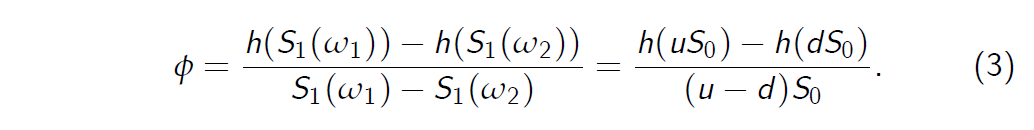

• Equality (3) is called the delta hedging formula.
  等式（3）称为 delta 套期保值公式
• One can substitute (3) into (1) or (2) in order to compute x.
  可以将（3）代入（1）或（2）中以计算 x
• To derive a convenient representation for x, we introduce the notation
  为得出 x 的方便表示，我们引入了符号

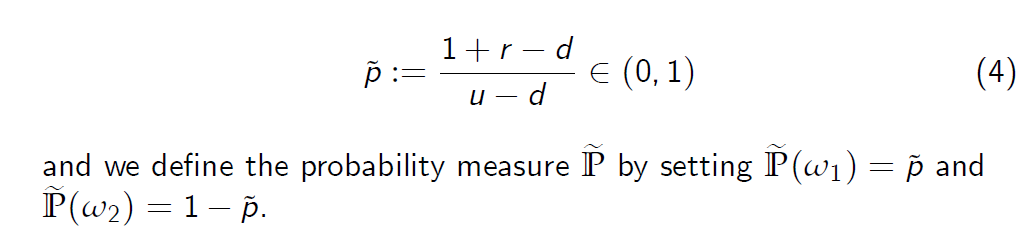
然后通过设置来定义概率测度

2.3 Pricing of a Contingent Claim

或有索取权的定价

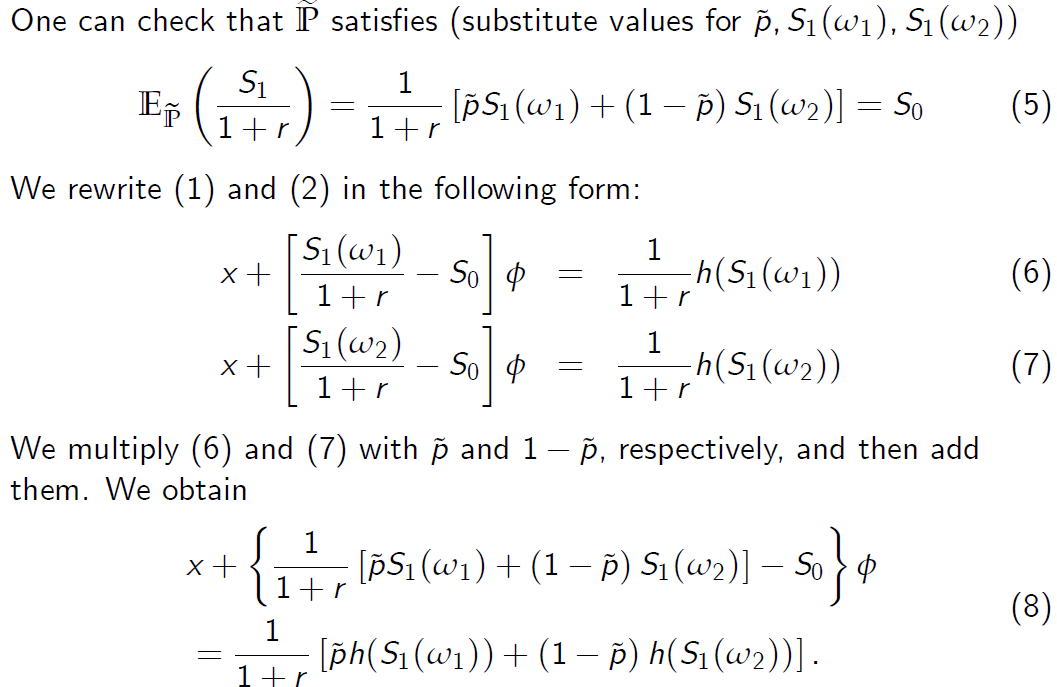
可以检查\( \mathbb {p}\)是否满足（\(\widetilde p\)的替代值） 我们以以下形式重写（1）和（2）： 我们将（6）和（7）分别乘以\(\widetilde p\)和\(1-\widetilde p\)，然后它们相加。 我们获得

2.4 Market Completeness

市场完整性

• In view of (5), the term with f vanishes. Therefore, equation (8) yields the following convenient representation for the price x
  根据（5），带有f的项消失。因此，等式（8）得出价格x的以下便捷表示形式

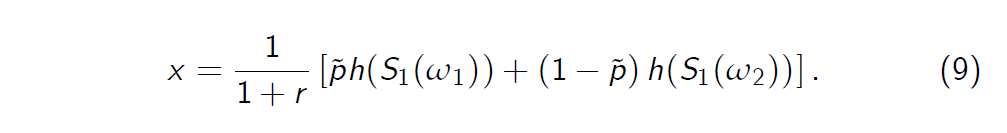
• It can be seen from (9) that the price x depends on \(\widetilde p\) and \(1 - \widetilde p\), but it is independent of the probabilities p and 1 - p.
  从（9）中可以看出，价格x取决于\(\widetilde p\)和\(1 - \widetilde p\)，但它与概率p和1-p无关。

• Note that equalities (3) and (9) hold for an arbitrary payoff function \(h(S_1)\). Hence for any contingent claim X we have found the unique replicating strategy and arbitrage price.
  请注意，等式（3）和（9）适用于任意收益函数\(h(S_1)\)。因此，对于任何或有索赔X，我们都找到了独特的复制策略和套利价格。
  Definition (Completeness)
  Since all contingent claims (that is, all derivative securities) in the elementary market model have replicating strategies, the market described by this model is called complete.
  定义（完整性） 由于基本市场模型中的所有或有索取权（即所有衍生证券）都具有复制策略，因此该模型描述的市场称为“完全”市场。

3.Risk-Neutral Probability Measure

  风险中性概率测度

3.1 Risk-Neutral Probability Measure

Definition (Risk-Neutral Probability Measure) A probability measure \(\mathbb Q\) on the sample space \(\Omega = \{\omega_1,\omega_2\}\) is called a risk-neutral probability measure (or an equivalent martingale measure) for the market model M= (B, S) if \(\mathbb Q\) is equivalent to \(\mathbb P\)and the following equality holds
样本空间\(\Omega = \{\omega_1,\omega_2\}\)上的概率测度\(\mathbb Q\)称为“风险中性概率测度”（风险中性概率测度**）对于市场模型M =（B，S）如果\(\mathbb Q\)等于\(\mathbb P\)且以下等式成立

\[\\\\ \mathbb E_ \mathbb Q(\frac{S_1}{1+r})=S_0\]

Proposition (3.2) 定义
The risk-neutral probability measure for the market model M= (B, S) is unique and it satisfies \(\mathbb Q = \tilde{\mathbb {P}}\) if and only if d < 1 + r < u.
市场模型 M =（B，S）的风险中性概率度量是唯一的，并且当且仅当 d <1 + r <u 时，它才能满足\(\mathbb Q = \tilde{\mathbb {P}}\)

If \(1 + r \le d \) or \(u \le 1 + r \) then no risk-neutral probability exists.
如果\(1 + r \le d \) or \(u \le 1 + r \) 则不存在风险中性概率。

[命题证明 3.2]成功地观察到平等 意思是 后者等于
请注意，对于d = 1 + r或u = 1 + r，由（10）给出的概率测度Q是定义明确的，但它不等于\(\mathbb P\)。

3.2 Expected Rates of Return

预期收益率

• Assume that u < 1 + r < d. Then the risk-neutral probability measure \(\tilde{\mathbb {P}}\) exists and is unique.
  假设u <1 + r <d。 然后，风险中性概率测度 \(\tilde{\mathbb {P}}\) 存在并且是唯一的。
• The expected rate of return on the savings account B equals
  储蓄帐户B的预期收益率等于

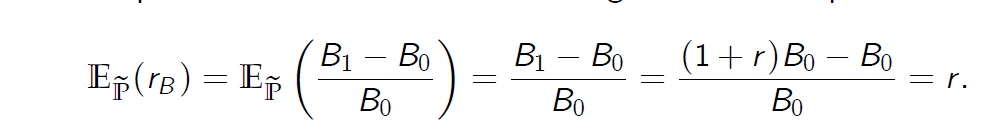
• The expected rate of return on the stock under \(\widetilde p\) equals r . This follows from the equality
  在\(\widetilde p\)下股票的预期收益率等于r。 这来自等式

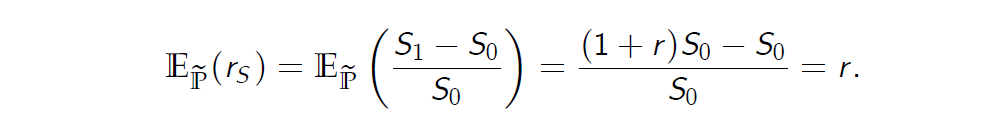
• The probability measure \(\tilde{\mathbb {P}}\) is the unique probability measure \(\mathbb Q\) under which the equality \(\mathbb E_\mathbb Q(r_B ) = \mathbb E_\mathbb Q(r_S )\) holds.
  等式\(\mathbb E_\mathbb Q(r_B ) = \mathbb E_\mathbb Q(r_S )\)在概率测度\(\tilde{\mathbb {P}}\)是唯一的概率测度\(\mathbb Q\)下成立。

3.3 Risk-Neutral Valuation Formula

风险中性估值公式
Proposition (3.3) For any claim \(X = h(S_1)\), the arbitrage price of X at time 0 in the arbitrage-free elementary market model M= (B, S) satisfies
定义（3.3） 对于任意债权 \(X = h(S_1)\)，无套利基本市场模型M=（B，S）中X在0时刻的套利价格满足

3.4 Proof.

[Proof of Proposition 3.3] We know (see (9)) that the price x satisfies
[命题证明 3.3]我们知道（见（9））价格x满足

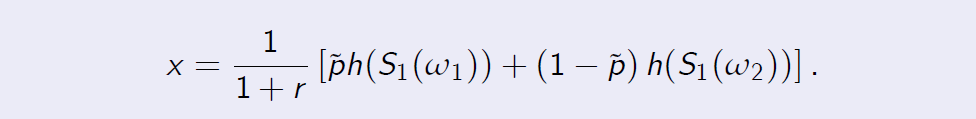
Formula (11) now follows immediately.
现在立即可以遵循公式（11）
We will now give another proof for (11).
现在我们将为（11）给出另一个证明。

Proof. [Another Proof of Proposition 3.3] It is assumed that u < 1 + r < d. Let \((x, \phi)\) be any trading strategy. From the equality
证明。 [另一个命题证明 3.3]假设u <1 + r <d。 令\((x, \phi)\)是任何策略交易。

\(\frac {V_1(x,\phi)}{1+r} = x + \phi (\frac {S_1} {1+r}-S_0)\) and formula (5), we deduce that investing is a ‘fair game’ under P meaning that: for any strategy \((x, \phi)\) we have
和公式（5），我们推论投资是P下的“公平博弈”，这意味着：对于任何策略\((x, \phi)\)，我们都有

\[E_\widetilde p (\frac {V_1(x,\phi)}{1+r})=x\]

In particular, if \((x, \phi)\) replicates X then \(V_1 (x, \phi) = X\) and thus we obtain the risk-neutral valuation formula (11)
特别是，如果\((x, \phi)\)复制X，则\(V_1 (x, \phi) = X\)，因此我们得到风险中性的估值公式（11）

4.Put-Call Parity Relationship

  买卖权平价关系

4.1 Example: Call and Put Options

示例：看涨期权和看跌期权

• Consider the elementary market model M= (B, S) with parameters
  考虑带参数的基本市场模型 M=（B，S）
  \(r = \frac {1}{3} ,S_0 = 1, u = 2, d = \frac {1}{2}, p = \frac{3}{5} and T = 1.\)

• Recall that the risk-neutral probability measure \(\tilde{\mathbb {P}}\) is given as
  回想一下，风险中性概率测度\(\tilde{\mathbb {P}}\)如下所示
  \(\tilde{\mathbb {P}} (\omega_1) = \widetilde p \ and \ \tilde{\mathbb {P}}(\omega_2) = 1 - \widetilde p\)
  where
  \(\widetilde p := \frac {1+r-d}{u-d}\)

• Hence the risk-neutral probability measure \(\tilde{\mathbb {P}}\) equals
  因此，风险中性概率测度\(\tilde{\mathbb {P}}\)等于

\[\tilde{\mathbb {P}}(\omega_1) = \widetilde p = \frac{1+\frac{1}{3}-\frac{1}{2}}{2-\frac{1}{2}}=\frac{5}{9}\]

and

\[\tilde{\mathbb {P}}(\omega_2) = 1-\widetilde p =\frac{4}{9}\]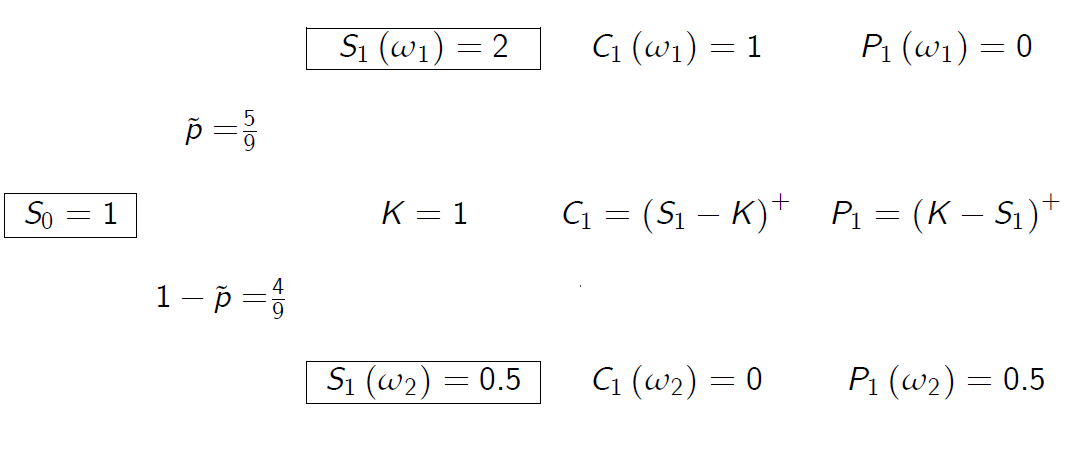

• 执行价K=1的欧式看涨期权的价格等于
• 执行价K=1的欧式看跌期权的价格等于

4.2 Put-Call Parity

买卖权平价关系

• The arbitrage prices at time 0 computed in Example (3.1) satisfy
  示例（3.1）中计算的时间0的套利价格满足

\[C_0-P_0=\frac{1}{4}= 1-\frac {3}{4} =S_0-\frac {1}{1+r} K \ \ \ \ (12)\]

• Equality (12) is a special case of the put-call parity.
  等式（12）是买卖权平价关系关系的一个特殊的情况

定义（3.4）
对于t = 0，1，买卖权平价关系可以表示如下
这里零息债券等于B

• Recall that we have already checked that \(C_T - P_T = S_T - K\) where T is the expiration date.
  回想一下，我们已经确认了\(C_T - P_T = S_T - K\) ，其中T是到期日期。
• Equality (13) is an easy consequence of Proposition (3.3).
  等式（13）是命题（3.3）的简单结果。

5.Summary of the Elementary Market Model

  基本市场模型概述

5.1 Summary: Properties

摘要：定义 Let us summarise the properties of the elementary market model:
让我们总结一下基本市场模型的属性：

1. The two-state single-period market model M= (B, S) is arbitrage-free if and only if d < 1 + r < u.
   且仅当d <1 + r <u 时，两组单周期市场模型 M =（B，S）是无套利的。
2. The arbitrage-free property of the model M= (B, S) does not depend on the actual probability measure \(\mathbb {P}\).
   模型 M =（B，S）的无套利性质不取决于实际概率测度P。
3. An arbitrary contingent claim X can be replicated by means of a unique trading strategy (hence the model is complete).
   可以通过独特的交易策略来复制任意或有债权X（因此模型是完整的）。
4. The initial endowment of a replicating strategy for X is called the arbitrage price for X and is denoted as \(\pi_0(X)\).
   X的复制策略的初始end赋称为X的套利价格，并表示为\(\pi_0(X)\)
5. The risk-neutral probability measure \(\tilde{\mathbb {P}}\) exists and is unique if and only if d < 1 + r < u (that is, whenever the model M is arbitrage-free). By definition, \(\tilde{\mathbb {P}}\) is equivalent to \(\mathbb {P}\).
   当且仅当d <1 + r <u（即，模型M无套利时），风险中性概率测度 \(\tilde{\mathbb {P}}\)存在且唯一。根据定义，\(\tilde{\mathbb {P}}\)等效于\(\mathbb {P}\)。
6. The arbitrage price \(\pi_0(X)\) of any claim X can be computed from the risk-neutral valuation formula.
   任何期权X的套利价格\(\pi_0(X)\) 可以从风险中性估值公式计算得出。

5.2 Summary: Theorem

定理（3.1基本市场模型） 当且仅当d <1 + r < u，基本市场模型 M =（B，S）是无套利的。
可以复制任何或有债权X，因此市场是完整的。形式上，对于某些\(（x，\phi）\in R^2\)，\(X = V_1（x，\phi）\)。
如果d <1 + r < u， 那么任何或有债权X都会承认唯一套利价格 \(\pi_0（X）：= x，\) 其中\(X = V_1（x，\phi\)）。
当且仅当d <1 + r < u时，模型M的风险中性概率度量\(\tilde{\mathbb {P}}\)存在且唯一。
如果\(1 + r \leq d\)或\(u \leq 1 + r\)，则不存在风险中性概率。
如果d <1 + r < u， 则任何或有索取权 X 的套利价格 \(\pi_0（X）\)都满足.

6.Generalisation of the Elementary Market Model

  基本市场模型的一般化

We generalise the elementary market model by postulating that:
我们通过假定以下内容概括基本市场模型：

1. We still deal with two primary traded assets: B and S.
   我们仍然处理两种主要交易资产：B和S
2. The sample space \(\{\Omega = \omega_1,\omega_2, . . . ,\omega_k\}\) g where \(k \ge 3\).
   样本空间…其中
3. Hence \(S_1 = (S_1(\omega_1), . . . , S_1(\omega_k ))\) where, without loss of generality, we may assume that
   因此…其中，在不失一般性的前提下，我们可以假设 \(S_1(\omega_k ) < S_1(\omega_{k-1}) < ... < S_1(\omega_2) < S_1(\omega_1).\)
4. It can be checked directly that this model is arbitrage-free if and only if \(S_1(\omega_k ) < S_0(1 + r ) < S_1(\omega_1)\).
   当且仅当…时，可以直接检查此模型是否无套利。
5. The risk-neutral probability measure Q exists if and only if \(S_1(\omega_k ) < S_0(1 + r ) < S_1(\omega_1)\), but it is not unique if \(k \ge 3\).
   5.当且仅当…时，存在风险中立概率度量Q，但如果…。
6. The market is incomplete when \(k \ge 3\): for some contingent claims \(X = (X(\omega_1), . . . ,X(\omega_k )) \)no replicating strategy exists.
   当…：对于某些或有主张…没有复制策略时，市场是不完整的存在
7. We will not examine this model in detail, since it can be seen as a special case of a general single-period market model.
   我们将不详细研究此模型，因为它可以看作是一般单周期市场模型的特例。

基本市场模型的一般化
基本市场模型的一般化 定理（3.1基本市场模型）

• 当且仅当\(S_1（\omega_k）<S_0（1 + r）<S_1（\omega_1）\)时，广义基本市场模型 M =（B，S）是无套利的。
• 某些（但不是全部）或有要求可以被复制（即可以实现）。 因此，模型M =（B，S）是不完整的。
• 如果\(S_1（\omega_k）<S_0（1 + r）<S_1（\omega_1\)），则任何可达到的索赔X都具有唯一的套利价格\(\pi_0（X）\)。 当且仅当\(S_1（\omega_k）<S_0（1 + r）<S_1（\omega_1\)）时，才会存在模型 M 的风险中立概率度量Q 它不是唯一的。 如果\(S_1（\omega_k）<S_0（1 + r）<S_1（\omega_1\)，则任何可达到的索赔X的套利价格p0（X）都满足

\(\tilde{\mathbb {P}}\)