Unit 3 Single Period Market Model

  单期市场模型

Uploaded by eva

General Single-Period Market Model

  一般单期市场模型

• The main differences between the elementary and general single-period market models are:
  基本和一般单期市场模型的主要区别在于：

• The investor is allowed to invest in several risky securities instead of only one.
  投资者可以投资多种风险证券，而不是只投资一种。

• The sample set is bigger, that is, there are more possible states of the world at time t = 1.
  样本集越大，也就是说，在t=1时，世界的可能状态越多。

• The sample space is \(\Omega = \{\omega_1,\omega_2, . . . ,\omega_k\}\) with \(\cal F = 2^{\Omega}\).
  样本空间是

• An investor’s personal beliefs about the future behaviour of stock prices are represented by the probability measure \(\mathbb P( \omega_i ) = p_i > 0 \) for i = 1, 2, . . . , k.
  投资者对股票价格未来行为的个人信念由概率测度 \(\mathbb P( \omega_i ) = p_i > 0 \) 表示，i = 1, 2, . . . , k.

• The savings account B equals \(B_0 = 1\) and \(B_1 = 1 + r\) for some constant r > -1.
  对于某些常数 r > -1 储蓄账户B等于 \(B_0 = 1\) and \(B_1 = 1 + r\)

• The price of the jth stock at t = 1 is a random variable on \(\Omega\). It is denoted by \(S_t^{j}\) t for t = 0, 1 and j = 1, . . . , n.
  t=1时第j种股票的价格是\(\Omega\)上的随机变量。对于t=0，1和j = 1, . . . , n.

• A contingent claim \(X = (X(\omega_1), . . . ,X(\omega_k)\)) is a random variable on the probability space \((\Omega,\cal F,\mathbb P)\).
  一个或有索取权 \(X = (X(\omega_1), . . . ,X(\omega_k)\)) 是概率空间上的随机变量\((\Omega,\cal F,\mathbb P)\)。

Questions

1. Under which conditions a general single-period market model \(\cal M= (B, S^1, . . . , S^n)\) is arbitrage-free?
   在什么条件下，一般的单期市场模型\(\cal M= (B, S^1, . . . , S^n)\)是否无套利？

2. How to define a risk-neutral probability measure for a model?
   如何为模型定义风险中性概率度量？

3. How to use a risk-neutral probability measure to analyse a general single-period market model?
   如何使用风险中性概率测度来分析一般的单期市场模型？

4. Under which conditions a general single-period market model is complete?
   一般单期市场模型在哪些条件下是完整的？

5. Is completeness of a market model related to risk-neutral probability measures?
   市场模型的完全性是否与风险中性概率测度有关？

6. How to define an arbitrage price of an attainable claim?
   如何定义可实现债权的套利价格？

7. Can we still apply the risk-neutral valuation formula to compute the price of an attainable claim?
   我们是否仍然可以应用风险中性估价公式来计算可实现债权的价格？

8. How to deal with contingent claims that are not attainable?
   如何处理无法实现的未定权益？

9. How to use the class of risk-neutral probability measures to value non-attainable claims?
   如何使用风险中性概率度量来评估无法实现的债权？

Outline We will examine the following issues:

1 Trading Strategies and Arbitrage-Free Models

  交易策略与无套利模型

在一般的单周期市场模型中，投资者的交易策略（或投资组合）被定义为一个向量：

where x is the initial wealth of an investor and fj stands for the number of shares of the jth stock purchased at time t = 0.
式中，x是投资者的初始财富，\(\phi^j\)表示在t=0时购买的第j只股票的股数。

If an investor adopts the trading strategy \((x, \phi^1, . . . , \phi^n) \)at time t= 0 then the cash value of his portfolio at time t = 1 equals
如果投资者采用t=0时的交易策略\((x, \phi^1, . . . , \phi^n) \)那么他的投资组合在t=1时的现金价值等于

\[V_1(x, \phi^1, . . . , \phi^n) :=(x-\Sigma_{j=1}^{n} \phi^j S_{0}^j)(1+r)+\Sigma_{j=1}^{n} \phi^j S_{1}^j\]

1.1 Wealth Process of a Trading Strategy

交易策略的财富过程

交易策略的财富过程（或价值过程）\(V_0(x, \phi^1, . . . , \phi^n)\)是一对

实数\(V_0(x, \phi^1, . . . , \phi^n)\)是初始价值

实值随机变量\(V_1(x, \phi^1, . . . , \phi^n)\)表示t=1时投资组合的现金价值

1.2 Gains (Profits and Losses) Process

• Obviously, the proits or losses an investor obtains from the investment can be calculated by subtracting \(V_0(\cdot) \)from \(V_1(\cdot)\).This is called the (undiscounted) gains process.
  显然，投资者从投资中获得的利润或损失可以通过从 \(V_1(\cdot)\)中减去\(V_0(\cdot) \)来计算，这被称为（未贴现）收益过程。

• The ‘gain’ can be negative; hence it may also represent a loss.
  “收益”可以是负数，因此也可能代表损失。

收益过程定义为

其中，随机变量 \(\Delta S_1^j=S_1^j-S_0^j\) 表示第j种股票价格的名义变化。

1.3 Discounted Stock Price and Wealth Process

贴现股价与财富过程

• To understand whether the jth stock appreciates in real terms, we consider the discounted stock prices of the jth stock
  为了了解第 j 只股票是否实际升值，我们考虑了第 j 只股票的贴现股价

\[\hat S_{0}^j := S_{0}^j =\frac {S_{0}^j}{B_0}, \hat S_{1}^j :=\frac {S_{1}^j}{1+r} =\frac {S_{1}^j}{B_1}\]

• Similarly, we define the discounted wealth process as
  同样，我们将贴现财富过程定义为 \(\hat V_0(x,\phi^1,...,\phi^n) := x,    \hat V_1 (x,\phi^1,...,\phi^n) :=\frac {V_1 (x,\phi^1,...,\phi^n)}{B_1}\)

• It is easy to see that
  很容易看出这一点

\[\hat V_1(x,\phi^1,...,\phi^n)=(x-\Sigma_{j=1}^{n} \phi^j \hat S_1^j )+\Sigma_{j=1}^{n} \phi^j \hat S_1^j =x+\Sigma_{j=1}^{n} \phi^j (\hat S_1^j-\hat S_0^j)\]

1.4 Discounted Gains Process

贴现收益法

投资者的贴现收益过程定义为

式中，\(\Delta \hat S_1^j= \hat S_1^j- \hat S_0^j\)表示第 j 种股票贴现价格的变化。

1.5 Arbitrage: Definition

套利：定义

The concept of an arbitrage in a general single-period market model is essentially the same as in the elementary market model. It is worth noting that \(\mathbb P\) can be replaced here by any equivalent probability measure \(\mathbb Q\).
一般单期市场模型中的套利概念与基本市场模型中的套利概念基本相同。值得注意的是，这里\(\mathbb P\)可以用任何等价的概率测度\(\mathbb Q\)来代替。

交易策略\(（x, \phi^1, . . . , \phi^n\))在一般的单周期市场模型中，如果

1.6 Arbitrage: Equivalent Conditions

套利：等价条件

The following condition is equivalent to A.3.
以下条件相当于A.3

• A.3’. There exists \(\omega \in \Omega\) such that \(V_1(x, \phi^1, . . . , \phi^n)(\omega) > 0\).
  The definition of arbitrage can be formulated using the discounted value and gains processes. This is sometimes very helpful.

存在\(\omega \in \Omega\) 使得 \(V_1(x, \phi ^1, . . . , \phi^n)(\omega) > 0\)。

套利的定义可以用贴现价值和收益过程来表述。这有时很有帮助。

交易策略\(（x, \phi^1, . . . , \phi^n\)) 在一般的单期市场模型中，当且仅当下列条件之一成立时，才是套利机会：

1.假设A.1-A.3在套利持有的定义用 \(\hat V（x, \phi^1, . . . , \phi^n)\) 代替 \(V（x, \phi^1, . . . , \phi^n)\)
2.在套利的定义中，x=0和A.2-A.3用 \(\hat G_1（x, \phi^1, . . . , \phi^n)\) 代替 \(G_1（x, \phi^1, . . . , \phi^n)\)

[命题4.1的证明：第一步]我们将证明以下两种说法是正确的：

套利的定义与命题4.1中的条件1是等价的。

在命题4.1中，条件1等价于条件2

为了证明第一个陈述，我们使用\(V（x, \phi^1, . . . , \phi^n)\)与 \(\hat V（x, \phi^1, . . . , \phi^n)\) 两者的关系，那是，

这表明第一条语句成立。

[命题4.1的证明：第二步]为了证明第二个陈述，我们回顾

现在很清楚，对于x=0，我们有

因此，第二种说法也是正确的。

事实上，我们还可以观察到 \(\hat G（x, \phi^1, . . . , \phi^n)\)不完全依赖于x，因此…

1.7 Verification of the Arbitrage-Free Property

无套利财产的核实

• It can be sometimes hard to check directly whether arbitrage opportunities exist in a given market model, especially when dealing with several risky assets or in the multi-period setup.
  有时很难直接检查在给定的市场模型中是否存在套利机会，特别是在处理多个风险资产或在多期设置中。

• We have introduced the risk-neutral probability measure in the elementary market model and we noticed that it can be used to compute the arbitrage price of any contingent claim.
  我们在基本市场模型中引入了风险中性概率测度，并注意到它可以用来计算任何未定权益的套利价格。

• We will show that the concept of a risk-neutral probability measure is also a convenient tool for checking whether a general single-period market model is arbitrage-free or not.
  我们将证明风险中性概率测度的概念也是检验一般单期市场模型是否无套利的一个方便工具。

• In addition, we will argue that a risk-neutral probability measure can also be used for the purpose of valuation of a contingent claim (either attainable or not).
  此外，我们还将论证风险中性概率测度也可用于或有索取权（可实现或不可实现）的估价。

1.8 Risk-Neutral Probability Measure

风险中性概率测度

定义（风险中性概率测度）

对于一般单周期市场模型\(\cal M\)，概率测度\(\mathbb Q\)对\(\mathbb W\)称为风险中性概率测度，如果：

我们用\(\mathbb M\)表示单期市场模型\(\cal M\)的全部风险中性概率测度的类别。

• Condition R.1 means that \(\mathbb Q\) and \(\mathbb P\) are equivalent probability measures. A risk-neutral probability measure is also known as an equivalent martingale measure.
  条件R.1意味着 \(\mathbb Q\) 和 \(\mathbb P\) 是等价概率测度。风险中性概率测度也称为等价鞅测度

• Note that condition R.2 is equivalent to \(\mathbb E_Q (\hat S_1^j)= \hat S_0^j\)or, more explicitly,
  注意，条件R.2相当于…或者，更多明确地,

\[\mathbb E_Q (S_1^j)= (1+r) S_0^j\]

for j=1,2,…,n.

1.9 Example

Example 4.1: Stock Prices

• We consider the following model featuring two stocks \(S^1\) and \(S^2\) on the sample space \(\Omega = \{\omega_1,\omega_2,\omega_3\}\).
  我们考虑以下模型，在样本空间\(\Omega = \{\omega_1,\omega_2,\omega_3\}\)上有两个股票\(S^1\) and \(S^2\)

• The interest rate \(r = \frac{1}{10}\) so that \(B_0 = 1 \) and \(B_1 = 1 + \frac{1}{10} \).
  利率\(r = \frac{1}{10}\)，因此\(B_0 = 1 \)和\(B_1 = 1 + \frac{1}{10} \)

• We deal here with the market model \(M= (B, S^1, S^2)\).
  这里我们讨论的是市场模型 \(M= (B, S^1, S^2)\)

• The stock prices at t = 0 are given by \(S_0^1 = 2 \)and \(S_0^2 = 3\).
  t=0时的股票价格由\(S_0^1 = 2 \)and \(S_0^2 = 3\)给出

• The stock prices at t = 1 are represented in the table:
  t=1时的股价如下表所示：

	\(\omega_1\)	\(\omega_2\)	\(\omega_3\)
\(S_1^1\)	1	5	3
\(S_1^2\)	3	1	6

Example 4.1: Wealth Process

例4.1：财富过程

• For any trading strategy \((x, \phi^1, \phi^2) \in R^3\), we have

对于任何交易策略\((x, \phi^1, \phi^2) \in R^3\)，我们有

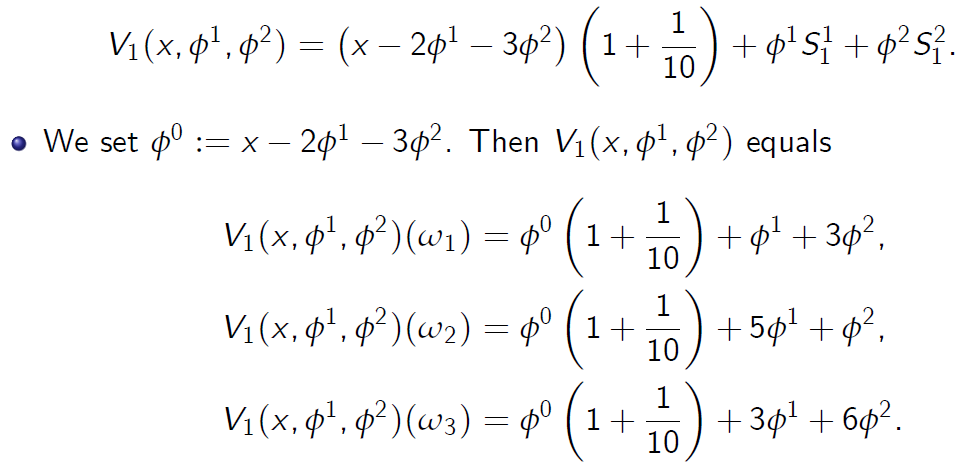
Example 4.1: Gains Process

例4.1:盈利过程

例4.1：财富过程

对于任何交易策略，我们有

Example 4.1: Discounted Stock Prices

例4.1：折扣股价

• Out next goal is to compute the discounted wealth process\(\hat V(x,\phi^1,\phi^2) \)and the discounted gains process \(\hat G_1(x,\phi^1,\phi^2) \).
  下一个目标是计算折现财富过程\(\hat V(x,\phi^1,\phi^2) \)和折现收益过程\(\hat G_1(x,\phi^1,\phi^2) \)

• To this end, we first compute the discounted stock prices.
  为此，我们首先计算股票的贴现价格。

• Of course, \(\hat S_0^j = S_0^j \) for j = 1, 2.
  当然，\(\hat S_0^j = S_0^j \) 表示 j = 1, 2

• The following table represents the discounted stock prices \(\hat S_1^j\) for j = 1, 2 at time t = 1
  下表显示了时间t=1时j=1，2的折扣股价\(\hat S_1^j\)

	\(\omega_1\)	\(\omega_2\)	\(\omega_3\)
\(\hat S_1^1\)	\(\frac {10}{11}\)	\(\frac {50}{11}\)	\(\frac {30}{11}\)
\(\hat S_1^2\)	\(\frac {30}{11}\)	\(\frac {10}{11}\)	\(\frac {60}{11}\)

Example 4.1: Discounted Wealth Process

贴现财富过程 The discounted wealth process \(\hat V (x, \phi^1, \phi^2)\) is thus given by

贴现财富过程 \(\hat V (x, \phi^1, \phi^2)\) 由

\[\hat V_0(x, \phi^1, \phi^2) = V_0(x, \phi^1, \phi^2) = x\]

and

\(\hat V_1(x, \phi^1, \phi^2)(\omega_1) = \phi^0+ \frac{10}{11} \phi^1+\frac{30}{11} \phi^2\)
\(\hat V_1(x, \phi^1, \phi^2)(\omega_2) = \phi^0+ \frac{50}{11} \phi^1+\frac{10}{11} \phi^2\)
\(\hat V_1(x, \phi^1, \phi^2)(\omega_3) = \phi^0+ \frac{30}{11} \phi^1+\frac{60}{11} \phi^2\)

where \(\phi^0 = x - 2\phi^1 - 3\phi^2\) is the amount of cash invested in B at time 0(as opposed to the initial wealth given by x).
式中，\(\phi^0 = x - 2\phi^1 - 3\phi^2\)是在时间0时投资于B的现金量（与x给出的初始财富相反）。

Example 4.1: Discounted Gains Process

示例4.1：贴现收益过程

• The increments of the discounted stock prices equal
  贴现股票价格的增量等于

因此折现收益 \(\hat G (x, \phi^1, \phi^2)\) 由下式给出

Example 4.1: Arbitrage-Free Property

无套利财产

• The condition \(\hat G_1(x, \phi^1, \phi^2) \ge 0\) is equivalent to
  条件\(\hat G_1(x, \phi^1, \phi^2) \ge 0\) 等价于

\(-12\phi^1 - 3\phi^2 \ge 0\)
\(28\phi^1 - 23\phi^2 \ge 0\) \(8\phi^1 + 27\phi^2 \ge 0\)

-Can we find \((\phi^1, \phi^2) \in R^2\) such that all inequalities are valid and at least one of them is strict?
我们能不能找到\((\phi^1, \phi^2) \in R^2\),使得所有的不等式都是有效的，并且其中至少有一个是严格的？

• It appears that the answer is negative, since the unique vector satisfying all inequalities above is \((\phi^1, \phi^2) = (0, 0)\).
  答案似乎是否定的，因为满足上述所有不等式的唯一向量是\((\phi^1, \phi^2) = (0, 0)\)

• Therefore, the single-period market model \(M= (B, S^1, S^2)\) is arbitrage-free.
  因此，单期市场模型 \(M= (B, S^1, S^2)\)是无套利的。

Example 4.1: Risk-Neutral Probability Measure

示例4.1：风险中性概率测度

• We will now show that this market model admits a unique risk-neutral probability measure on \(\Omega = \{\omega_1,\omega_2,\omega_3\}\).
  我们现在将证明这个市场模型在\(\Omega = \{\omega_1,\omega_2,\omega_3\}\) 上有唯一的风险中性概率测度。

• Let us denote \(Q(\omega_i ) = q_i\) for i = 1, 2, 3. From the definition of a risk-neutral probability measure, we obtain the following linear system
  让我们表示\(\mathbb Q(\omega_i ) = q_i\)，i=1，2，3。从风险中性概率测度的定义出发，我们得到如下线性系统

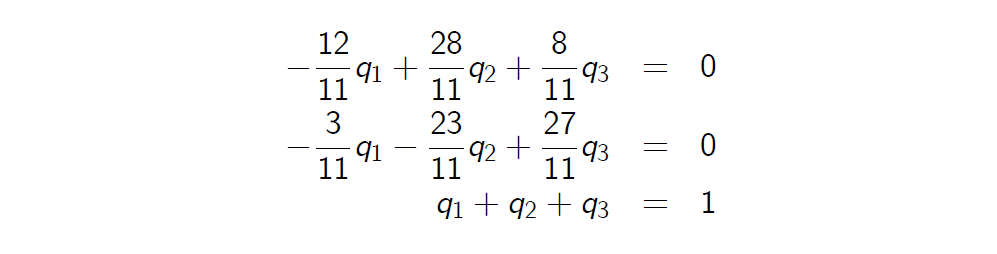
• The unique solution equals \(\mathbb Q = (q_1, q_2, q_3) = (\frac{47}{80},\frac{15}{80},\frac{18}{80})\)
  唯一解等于

2 Fundamental Theorem of Asset Pricing

资产定价基本定理

2.1 Fundamental Theorem of Asset Pricing (FTAP)

资产定价基本定理（FTAP）

• In Example 4.1, we have checked directly that the market model \(\cal M= (B, S^1, S^2)\) is arbitrage-free.
  在示例4.1中，我们直接检查了市场模型\(\cal M= (B, S^1, S^2)\)是否无套利。
• In addition, we have shown that the unique risk-neutral probability measure exists in this model.
  此外，我们还证明了该模型存在唯一的风险中性概率测度

• Is there any relation between no arbitrage property of a market model and the existence of a risk-neutral probability measure?
  市场模型的无套利性与风险中性概率测度的存在是否有关系？

• The following important result, known as the FTAP, gives a complete answer to this question within the present setup.
  下面的重要结果称为FTAP，在当前设置中给出了这个问题的完整答案
• The FTAP was first established by Harrison and Pliska (1981) and it was later extended to continuous-time market models.
  FTAP最初由Harrison和Pliska（1981）建立，后来扩展到连续时间市场模型。

定理（FTAP)
一般单周期市场模型\(\cal M= (B, S^1, S^2)\)是无套利的当且仅当\(\cal M\) 存在一个风险中性概率测度，即 \(\mathbb M\)

证明
证明是可选的，在这组幻灯片的末尾给出。很容易证明，如果所有风险中性概率测度\(\mathbb M\)的集合不为空，则不存在套利。相反陈述的证明要困难得多。

3 Examples of Market Models

3 市场模型示例

Example 4.1: Arbitrage-Free Market Model

例4.1：无套利市场模型

• We consider the market model \(\cal M= (B, S^1, S^2) \)introduced in Example 4.1.
  我们考虑示例4.1中引入的市场模型\(\cal M= (B, S^1, S^2) \)

• The interest rate \(r = \frac{1}{10}\) so that \(B_0 = 1\) and \(B_1 = 1 + \frac {1}{10}\).
  利率 \(r = \frac{1}{10}\)，因此\(B_0 = 1\) and \(B_1 = 1 + \frac {1}{10}\).

• The stock prices at t = 0 are given by \(S_0^1 = 2\) and \(S_0^2= 3\).
  t=0时的股票价格由\(S_0^1 = 2\)和\(S_0^2= 3\)给出。

• We have shown that the increments of the discounted stock prices \(\hat S^1\) and \(\hat S^2\) equal
  我们已经证明了贴现股票价格\(\hat S^1\)和\(\hat S^2\)的增量相等

• How to find RNP measure?
  如何找到风险中性概率测度？

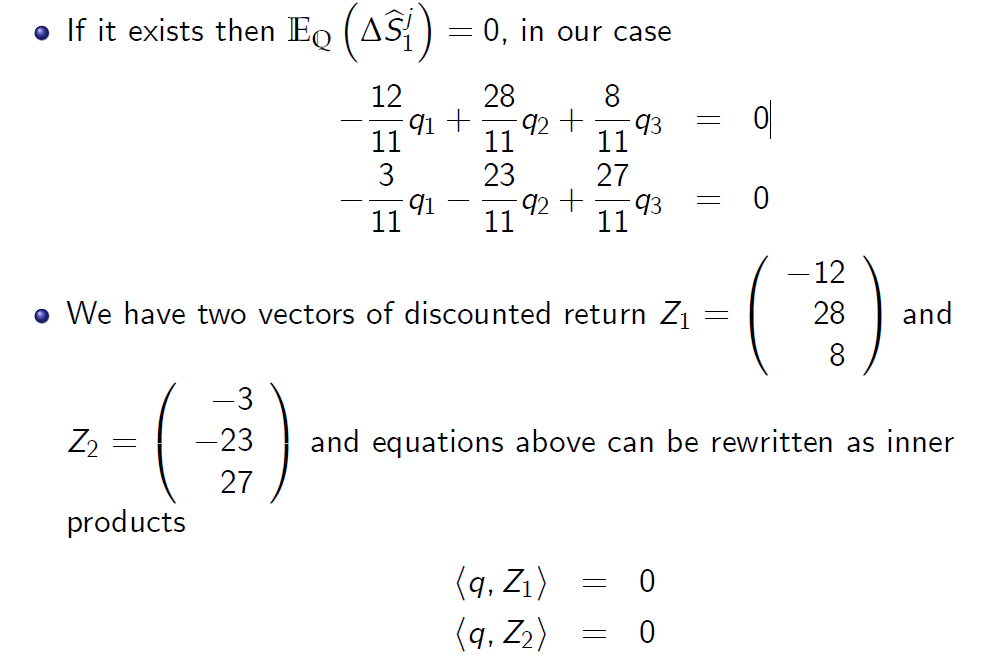
如果它存在，那么\(E_Q(\Delta \hat S_1^j)=0\)，在我们的例子中
我们有两个贴现回报向量和上面的等式可以重写为内积

• The gain expressions
  增益表达式

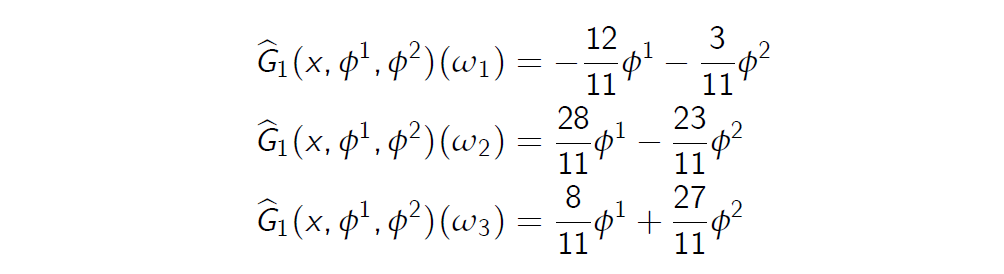
determines a hyperplane in \(R^3: \phi^1 Z_1 + \phi^2 Z_2, \phi^1, \phi^2 \in R \)
确定\(R^3: \phi^1 Z_1 + \phi^2 Z_2, \phi^1, \phi^2 \in R \) 中的超平面

• So, vector \(q : \langle q,Z_j \rangle = 0 \) must be orthogonal to the hyperplane.
  所以，向量\(q : \langle q,Z_j \rangle = 0 \) 必须与超平面垂直。

• And \(\Sigma_i^K q_i =1, q_i \gt 0\)

• If such vector exists then it defines RNP measure.
  如果这样的向量存在，那么它定义RNP测度。

• For our example there is the unique risk-neutral probability measure.
  对于我们的例子，有唯一的风险中性概率测度。

• The FTAP confirms that the market model is arbitrage-free.
  FTAP证实了市场模型是无套利的。

• We consider the following model featuring two stocks \(S^1\) and \(S^2\) on the sample space \(\Omega = \{\omega_1,\omega_2,\omega_3\}\).
  我们考虑样本空间\(\Omega = \{\omega_1,\omega_2,\omega_3\}\) 上具有两个股票\(S^1\) 和 \(S^2\)的以下模型。

• The interest rate \(r = \frac{1}{10} \) so that \(B_0 = 1 \)and \(B_1 = 1 + \frac {1}{10} \).
  利率 \(r = \frac{1}{10} \) 因此 \(B_0 = 1 \) 和 \(B_1 = 1 + \frac {1}{10} \)

• The stock prices at t = 0 are given by \(S_0^1 = 1\) and \(S_0^2 = 2\) and the stock prices at t = 1 are represented in the table:
  t=0时的股票价格由\(S_0^1 = 1\) 和 \(S_0^2 = 2\)给出，t=1时的股票价格如下表所示：

• Does this market model admit an arbitrage opportunity?
  这种市场模式是否允许套利机会？
• The increments of discounted stock prices are represented in the following table
  贴现股票价格的增量如下表所示

• To tell whether a model is arbitrage-free it su¢ ces to know the increments of discounted stock prices.
  要判断一个模型是否无套利，就必须知道贴现股价的增量。

• Recall that
  记得吗 \(\hat G_1(x,\phi^1,\phi^2) = \phi^1 \Delta \hat S_1^1 + \phi^2 \Delta \hat S_1^2\)

• Hence, the equation for hyperplane
  因此，超平面方程

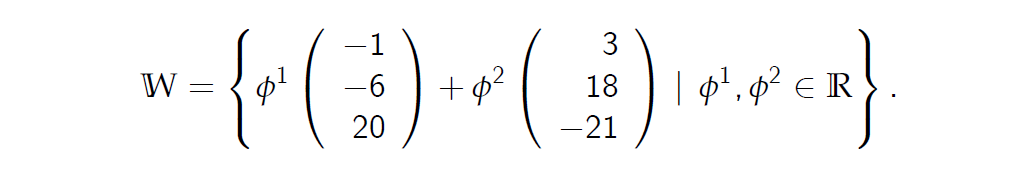
• Let us take \(\phi^1 = 3 \) and \(\phi^2 = 1\). Then we obtain the vector\((0, 0, 39)^T\) , which means we have an arbitrage opportunity.
  我们取\(\phi^1 = 3 \)和\(\phi^2 = 1\)。然后我们得到向量\((0, 0, 39)^T\)，这意味着我们有一个套利机会。

• Still, we can solve the system for the ‘orthogonal vector’:
  不过，我们可以解出“正交向量”的系统

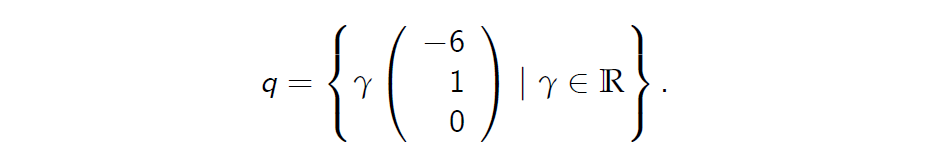
• but must have \(\mathbb Q(\omega) > 0 \) for all \(\omega \in \Omega\).
  但必须有

• Hence the FTAP confirms that the market model is not arbitrage-free.
  因此FTAP证实了市场模型不是无套利的。

4 Risk-Neutral Valuation of Contingent Claims

4 或有债权的风险中性估值

4.1 Contingent Claims

4.1或有债权

• Since we now know how to check whether a given model is arbitrage-free, the following question arises:
  由于我们现在知道如何检查给定模型是否无套利，因此出现了以下问题：
• What should be the ‘fair’ price of a European call or put option in a general single-period market model?
  在一般的单期市场模型中，欧洲看涨期权或看跌期权的“公平”价格应该是多少？
• In a general single-period market model, the idea of pricing European options can be extended to any contingent claim.
  在一般的单期市场模型中，欧式期权定价的思想可以推广到任何未定权益。

或有债权是一个随机变量 X，定义在 \(\Omega\) 上，表示到期日的收益。

• Derivatives nowadays are usually quite complicated and thus it makes sense to analyse valuation and hedging of a general contingent claim, and not only European call and put options.
  如今的衍生品通常相当复杂，因此分析一般未定权益的估值和套期保值是有意义的，而不仅仅是欧式看涨期权和看跌期权.

4.2 No-Arbitrage Principle

4.2 无套利原则

定义（复制和套利价格）

当\(V_1(x,\phi^1,\phi^2)\)时，交易策略\((x,\phi^1,\phi^2)\)被称为期权 X 的复制策略（对冲策略）。初始财富也被表示为\(\Pi_0（X）\)，称为X的套利价格。

命题（无套利原则）
假设或有债权 X 可以通过交易策略的平均值\((x,\phi^1,\phi^2)\)复制。那么符合无套利原理的 X 在0 处的唯一价格等于\(V_0(x,\phi^1,\phi^2)=x\)。

证明
如果X的价格高于（低于）x，人们可以卖空（买入）X 并买入（卖空）复制投资组合。这将在扩展市场中产生一个套利机会，其中X在t=0时进行交易。

Example 4.3: Stochastic Volatility Model

随机波动模型

• In the elementary market model, a replicating strategy for any contingent claim always exists. However, in a general single-period market model, a replicating strategy may fail to exist for some claims.
  在基本市场模型中，任何或有债权总是存在一个复制策略。然而，在一个一般单周期市场模型中，复制策略可能不存在于某些债权。
• For instance, when there are more sources of randomness than there are stocks available for investment then replicating strategies do not exist for some claims.
  例如，当随机性的来源多于可供投资的股票时，某些债权就不存在复制策略。
• Consider a market model consisting of bond B, stock S, and a random variable v called the volatility.
  考虑一个由债券B、股票S和一个称为波动率的随机变量v组成的市场模型。
• The volatility determines whether the stock price can make either a big or a small jump.
  股票价格的波动性决定了任一股票价格是可以大幅上涨还是小幅上涨。
• This is a simple example of a stochastic volatility model.
  这是随机波动率模型的一个简单例子。
• The sample space is given by
  样本空间由 \(\Omega = \\{\omega_1,\omega_2,\omega_3,\omega_4\\}\) and the volatility is defined as

\[v (\omega_i)= \left \lbrace \begin{array}{l} h,\text{for}\ i = 1,4, \\\\ l,\text{for}\ i = 2,3. \end{array} \right.\]

• We furthermore assume that \(0 < l < h < 1\). The stock price \(S_1\) is given by
  我们进一步假设\(0 < l < h < 1\)。股票价格\(S_1\)是 \(S_1 (\omega_i)= \left \lbrace \begin{array}{l} (1+v(\omega_i))S_0,\text{for}\ i = 1,2, \\\\ (1-v(\omega_i))S_0,\text{for}\ i = 3,4. \end{array} \right.\)

• Unlike in examples we considered earlier, the amount by which the stock price in this market model jumps is random.
  与前面的例子不同，这个市场模型中股票价格的跳跃量是随机的。

• It is easy to check that the model is arbitrage-free whenever \(1 - h < 1 + r < 1 + h\).
  当\(1 - h < 1 + r < 1 + h\) 时，很容易检验模型是否无套利。

• We claim that for some contingent claims a replicating strategy does not exist. In that case, we say that a claim is not attainable.
  我们认为，对于某些未定权益，不存在复制策略。在这种情况下，我们说债权是不可实现的。

• To justify this claim, we consider the digital call option X with the payoff
  为了证明这一说法的合理性，我们考虑了数字看涨期权 X 的回报

\[X= \left \lbrace \begin{array}{l} 1 \ \text{if}\ S_1 \gt K, \\\\ 0 \ otherwise. \end{array} \right.\]

where K > 0 is the strike price.
其中 K>0 是行权价格。

• We assume that \((1 + l )S_0 < K < (1 + h)S_0\), so that
  我们假设\((1 + l )S_0 < K < (1 + h)S_0\), 因此

\((1 - h)S_0 < (1 - l )S_0 < (1 + l )S_0 < K < (1 + h)S_0\) and thus

\[X(\omega_i)= \left \lbrace \begin{array}{l} 1 \ \text{for}\ i=1, \\\\ 0 \ otherwise. \end{array} \right.\]

Suppose that \((x, \phi) \)is a replicating strategy for X. Equality\(V_1(x, \phi) = X\) becomes

假设\((x, \phi) \)是 X 的复制策略。等式 \(V_1(x, \phi) = X\) 变为

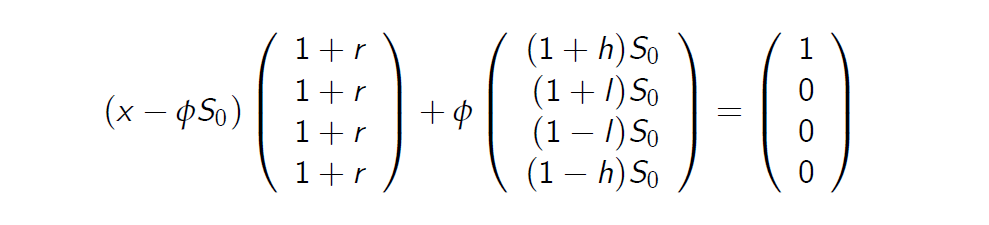
• two unknowns, four equations
  两个未知数，四个方程

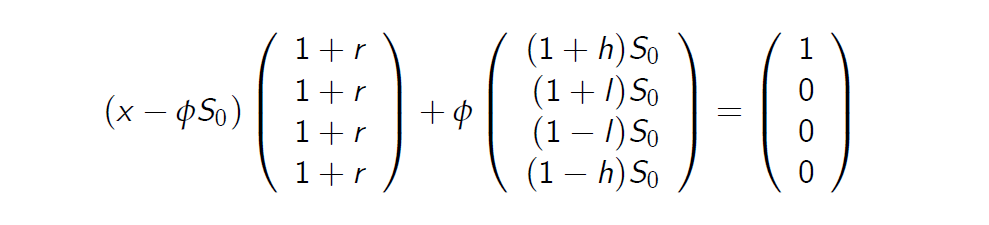
• It is easy to see that the above system of equations has no solution and thus a digital call is not an attainable contingent claim within the framework of the stochastic volatility model.
  不难看出，上述方程组没有解，因此在随机波动率模型的框架内，数字看涨期权不是可获得的未定权益。

• The heuristic explanation is that the randomness generated by the volatility cannot be replicated, we do not have anough traded assets to replicate volatility, since the volatility itself is not a traded asset in this model.
  启发式解释是，波动率产生的随机性无法复制，我们没有足够的交易资产来复制波动率，因为波动率本身在这个模型中不是交易资产。

4.3 Valuation of Attainable Contingent Claim

4.3 可实现或有债权的估价
We first recall the definition of attainability of a contingent claim.
我们首先回顾未定权益可得性的定义。

定义（可实现的未定权益）

如果存在X的复制策略，则称未定权益X为可实现的。

Let us summarise the known properties of attainable claims:
让我们总结一下可实现权利要求的已知性质：

• It is clear how to price attainable contingent claims by the replicating principle.
  如何用复制原则对可实现的未定权益进行定价是很清楚的。
• There might be more than one replicating strategy, but no arbitrage principle leads the initial wealth x (and therefore, price) to be unique.
  可能有不止一种复制策略，但没有套利原则导致初始财富 x（因此，价格）是唯一的。
• In the two-state single-period market model, one can use the risk-neutral probability measure to price contingent claims.
  在两状态单期市场模型中，可以使用风险中性概率测度对未定权益进行定价。

4.4 Risk-Neutral Valuation Formula

4.4 风险中性估值公式

Our next goal is to extend the risk-neutral valuation formula to any attainable contingent claim within the framework of a general single-period market model.
我们的下一个目标是在一般单期市场模型的框架内，将风险中性估值公式推广到任何可实现的或有权益。

命题（4.2）

设 X 为可得未定权益，\(\mathbb Q \in \mathbb M\) 为风险中性概率测度。那么 t=0 时 X 的套利价格等于\(V_1 (x,\phi^i,\phi^n)\)。

证明。

[命题4.2的证明] 回想一下交易策略\(x，\phi^i,\phi^n\) 是 X 的复制策略，只要 \(V_1 (x,\phi^i,\phi^n)\)

Example 4.3: Stochastic Volatility Model

例4.3：随机波动率模型

• Proposition 4.2 shows that risk-neutral probability measures can be used to price attainable contingent claims.
  命题4.2表明，风险中性概率测度可用于对可实现的未定权益进行定价。
• Consider the market model introduced in Example 4.3 with the interest rate r = 0.
  考虑示例4.3中引入的市场模型，利率r=0。
• Recall that in this case the model is arbitrage-free since \(1 - h < 1 + r = 1 < 1 + h\).
  回想一下，在这种情况下，模型是无套利的，因为\(1 - h < 1 + r = 1 < 1 + h\)。
• The increments of the discounted stock price bS are represented in the following table
  贴现股票价格\(\hat S\)的增量如下表所示

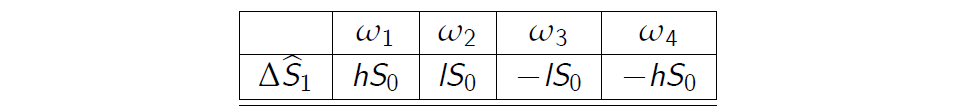
• The equation for ‘hyperplane’
  “超平面”方程

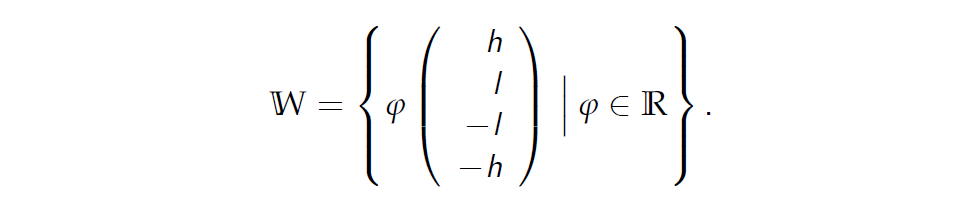
so it is not a hyperplane which must be the plane of maximim dimension.
所以它不是一个超平面，它必须是最大维的平面。

• The orthogonal complement of W is thus the three-dimensional subspace of \(\mathbb R^4\) given by
  因此，\(\mathbb W\) 的正交补是\(\mathbb R^4\)的三维子空间，由

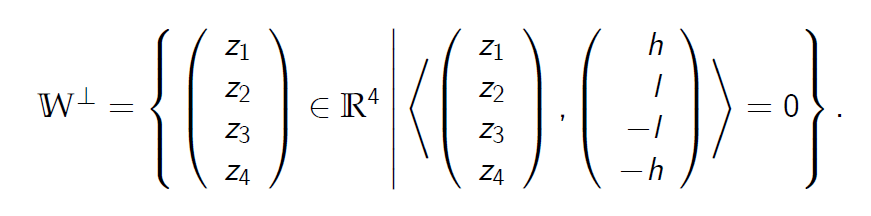
• Recall that a vector \((q_1, q_2, q_3, q_4)^T \)must satisfy \(\Sigma_{i=1}^4\)=1 holds and \(q_i > 0 \) for i = 1, 2, 3, 4.

回想一下，向量\((q_1, q_2, q_3, q_4)^T \) 必须满足 \(\Sigma_{i=1}^4\)=1 保持和 \(q_i > 0 \) for i = 1, 2, 3, 4.

• Specifically,
  具体来说，

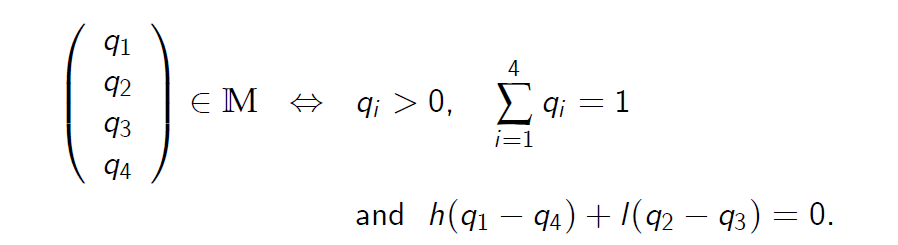
• The class \(\mathbb M\) of all risk-neutral probability measures in our stochastic volatility model is therefore given by
  因此，我们的随机波动率模型中所有风险中性概率测度的 \(\mathbb M\) 类由下式给出：

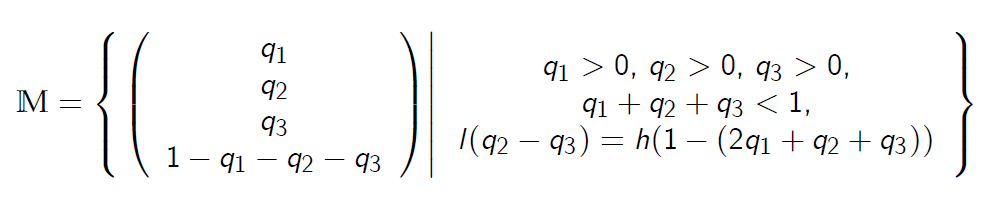
• This set appears to be non-empty and thus we conclude that our stochastic volatility model is arbitrage-free.
  这个集合似乎是非空的，因此我们得出结论，我们的随机波动率模型是无套利的。

• Recall that we have already shown that the digital call option is not attainable if
  回想一下，我们已经证明，如果 \((1+l)S_0 \lt K \lt (1+h)S_0\)

• It is not difficult to check that for every \(0 < q_1 < \frac{1}{2}\) there exists a probability measure \(\mathbb Q \in \mathbb M\) such that \(\mathbb Q(w_1) = q_1\).
  不难检查，对于每一个\(0 < q_1 < \frac{1}{2}\),存在一个概率度量\(\mathbb Q \in \mathbb M\) 使得\(\mathbb Q(w_1) = q_1\)。
• Indeed, it suffices to take \(q_1 \in (0, \frac{1}{2})\) and to set
  事实上，它足够取\(q_1 \in (0, \frac{1}{2})\) 和设置

\[q_4 = q_1, q_2 = q_3 = \frac{1}{2} - q_1\]

• We apply the risk-neutral valuation formula to the digital call \(X = (1, 0, 0, 0)^T\). For \(\mathbb Q = (q_1, q_2, q_3, q_4)^T \in \mathbb M \), we obtain
  我们将风险中性估值公式应用于数字看涨期权 \( X = (1, 0, 0, 0)^T\).为了\(\mathbb Q = (q_1, q_2, q_3, q_4)^T \in \mathbb M \),我们得到

\(\mathbb E_\mathbb Q(X) = q_1 \cdot 1 + q_2 \cdot 0 + q_3 \cdot 0 + q_4 \cdot 0 = q_1.\)

• Since \(q_1\) is any number from (0, 12), we see that every value from the open interval \((0, \frac{1}{2})\) can be achieved.
  由于\(q_1\)是（0，12）中的任意数字，我们可以看到开放区间\((0, \frac{1}{2})\)中的每个值都可以实现。

4.5 Extended Market Model and No-Arbitrage Principle

4.5 扩展市场模型和无套利原则
We no longer assume that a contingent claim X is attainable.
我们不再假定或有债权X是可以实现的。

如果存在由债券B，原始股票\(S^1,…,S^n\),以及满足\(S_0^{n+1}=\pi_0（X）\)和\(S_1^{n+1}=X\) 的附加资产\(S^{n+1}\)组成的扩展模型是无套利的，则称或有索取权 X 的价格\(\pi_0（X）\)符合无套利原则。

• The interpretation of Definition 4.1 is as follows:
  定义4.1的解释如下：

• We assume that the market model \(\cal M= (B, S^1, . . . , S^n)\) is arbitrage-free.
  我们假设市场模型\(M= (B, S^1, . . . , S^n)\) 是无套利的。
• We regard the additional asset as a tradable risky asset in the extended market model \(\widetilde M= (B, S^1, . . . , S^{n+1})\).
  我们认为额外资产作为交易风险资产在扩展市场模型 \(\widetilde M= (B, S^1, . . . , S^{n+1})\)
• We postulate its price at time 0 should be selected in such a way that the extended market model \(\widetilde M \) is still arbitrage-free.
  我们假设它在时间0的价格应该以这样一种方式选择，即扩展市场模型\(\widetilde M \)仍然是无套利的。

4.6 Valuation of Non-Attainable Claims

4.6无法实现的债权的估价

• We already know that the risk-neutral valuation formula returns the arbitrage price for any attainable claim.
  我们已经知道，风险中性估值公式返回任何可实现索赔的套利价格。
• The next result shows that it also yields a price consistent with the no-arbitrage principle when it is applied to any non-attainable claim.
  下一个结果表明，当它适用于任何不可实现的索赔时，它也产生了一个符合无套利原则的价格。
• The price obtained in this way is not unique, however.
  然而，以这种方式获得的价格并不是唯一的。

命题（4.3）

设 X 是一个可能不可得的或有索取权，\(\mathbb Q \)是一个任意的风险中性概率测度。则\(\pi_0（X）\)由

定义t=0时或有索取权的价格，符合无套利原则。

证明。 [命题4.3的证明]假设\(\mathbb Q \in \mathbb M\)是原始市场模型\(\cal M\)的任意风险中性概率测度。

对于\(S_0^{n+1}=\pi_0(X)\)和\(S_1^{n+1}=X\)的扩展市场模型\(\widetilde M=（B，S^1,…,S^{n+1}）\)，我们将展示 \(\mathbb Q\)也是一个风险中性概率测度

因此\(\mathbb Q \in \widetilde M\)确实是一个风险中性的概率度量在扩展市场模型中。

根据资产定价的基本定理，扩展市场模型\(\widetilde M\)是无套利的。因此，（2）给出的价格\(\pi_0（X）\)符合无套利原则。

5 Completeness of Market Models

5 市场模型的完整性

5.1 Models of Complete and Incomplete Markets

5.1完全市场和不完全市场模型

We categorise market models into two classes: complete and incomplete market models.
我们将市场模型分为两类：完全和不完全市场模型。

用一个模型描述的金融市场，如果任何未定权益 X 存在一个复制策略\(（x,\phi）\in R^{n+1}\)，则称为完全市场。当存在一个不存在复制策略的索赔X时，市场是不完整的。

• Given an arbitrage-free and complete markets, the issue of pricing contingent claims is completed solved.
  在无套利完全市场条件下，未定权益定价问题完全解决。
• How can we recognize whether a given market is complete?
  我们如何才能认识到一个给定的市场是否是完整的？

5.2 Algebraic Criterion for Market Completeness

市场完整性的代数判据

命题（4.4）

假设单周期市场模型\(\cal M=（B，S^1，S^n）\) 定义在样本空间\(\Omega =\{\omega_1,..\omega_k\}\)是无套利的。则M是完全的当且仅当k(n+1) 矩阵A

具有整个矩阵，即竖（A）=k。等价地，当线性子空间由向量\(A_0，A_1，…,A_n\)与全空间\(\mathbb R^k\)重合。

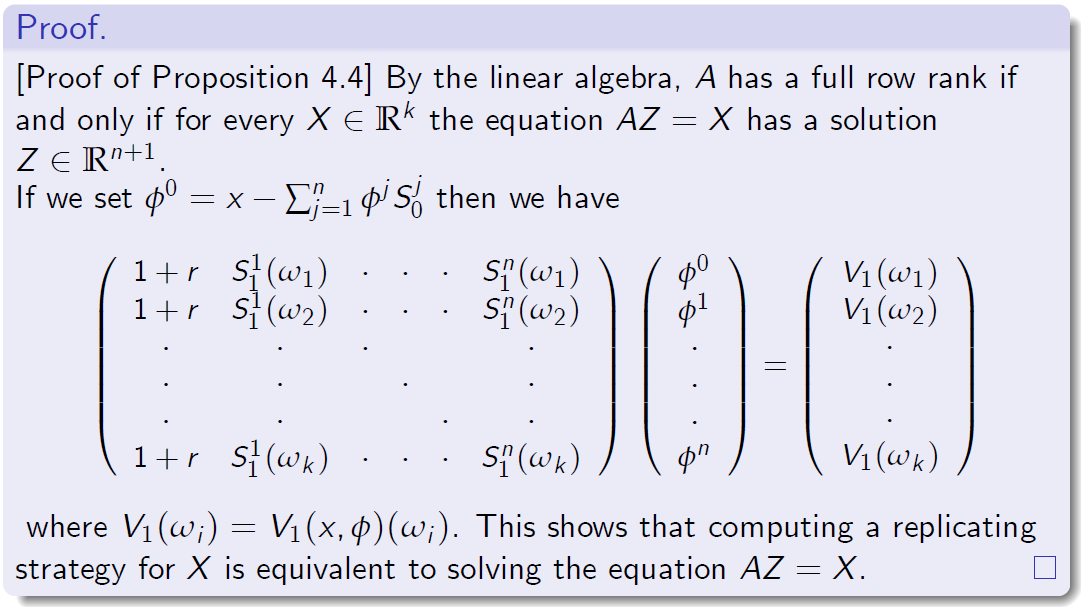
[命题4.4的证明]通过线性代数，A有一个全矩阵当且仅对于每一个\(X \in \mathbb R^k\)方程AZ=X 有一个解 \(Z\in R^{n+1}\)

式中\(V_1(\omega_i=V_1(x,\phi)(\omega_i)\)这表明，计算一个复制策略X是等价于求解方程AZ=X。

Example 4.3: Incomplete Market

例4.3：不完全市场

• Consider the stochastic volatility model from Example 4.3.
  考虑示例4.3中的随机波动率模型。

• We already know that this market is incomplete, since the digital call is not an attainable claim.
  我们已经知道这个市场是不完整的，因为数字称为一个不可实现的债权。

• The matrix A is given by

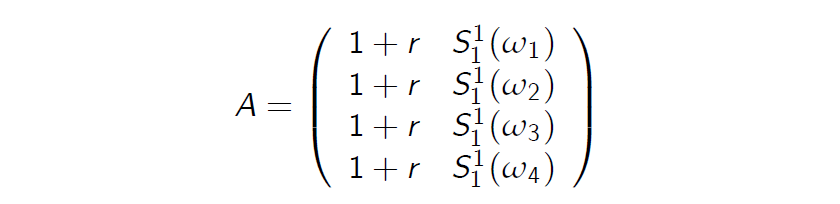
• The rank of A is 2, and thus it is not equal to k = 4.
  A的列是2，因此它不等于k=4
• In view of Proposition 4.4, this confirms that this market model is incomplete.
  鉴于命题4.4，这证实了这种市场模式是不完整的。

5.3 Probabilistic Criterion for Attainability

5.3可达性概率标准

• Proposition 4.4 yields a method for determining whether a market model is complete.
  命题4.4给出了一种确定市场模型是否完整的方法。
• Given an incomplete model, how to recognize an attainable contingent claim?
  在一个不完整的模型下，如何确认一个可实现的未定权益？
• Recall that if a model M is arbitrage-free then the class \(\mathbb{M}\) is non-empty.
  回想一下，如果模型M是无套利的，那么集合\(\mathbb{M}\)是非空的。
  命题（4.5） 假设单周期市场模型\(M=（B，S^1，…,S^n）\)是无套利的。则或有索取权X可获得的当且仅当期望值

所有风险中性概率测度有相同的价值 \(\mathbb Q \in \mathbb M\)

5.4 Probabilistic Criterion for Market Completeness

完全市场的概率准则

定理（4.1）

假设单周期市场模型\(M=（B，S^1，…,S^n）\是无套利的。当且仅当集合M由单个元素组成，即存在唯一的风险中性概率测度时，模型M是完整的。

证明。

[定理4.1中（）的证明]由于M被假定为无套利的，因此根据FTAP，至少存在一个风险中性概率测度，即M类是非空的。

首先假设M的风险中性概率测度是唯一的。

那么命题4.5的条件对于任何索赔X都是微不足道的满足。

因此，任何权利要求X都是可以实现的，因此市场模型是完整的。

证明。

[定理4.1的证明]假设扁M是完整的，并考虑花M的任意两个风险中性概率测度Q 和 \(\hat Q\)，对于一个固定，但任意的，i=1,…,k，设或有索取权\(X^i\)为

由于现在假设M是完全的，所以或有索取权Xi是可以实现的。因此，从命题4.2可以看出

因为i是任意的，我们看到等式\(Q=\hat Q\)成立。

6 Summary

小结 Let us summarise the properties of single-period market models:
让我们总结一下单周期市场模型的特性：

• A single-period market model is arbitrage-free if and only if it admits at least one risk-neutral probability measure.
  -单期市场模型是无套利的当且仅当它至少允许一个风险中性概率测度。

• An arbitrage-free single-period market model is complete if and only if the risk-neutral probability measure is unique.
  当且仅当风险中性概率测度唯一时，无套利单期市场模型是完备的。

• Under the assumption that the model is arbitrage-free:
  假设模型无套利：

  • An arbitrary attainable contingent claim X (that is, a claim that can be replicated by means of some trading strategy) has the unique arbitrage price \(\pi_0(X)\).
    任意可得或有债权X（即，可以通过某种交易策略复制的债权）具有唯一的套利价格\(\pi_0(X)\)。

  • The arbitrage price \(\pi_0(X)\) of any attainable claim X can be computed from the risk-neutral valuation formula using any risk-neutral probability measure \(\mathbb{Q}\).
    任何可得索赔X的套利价格\(\pi_0(X)\)可以使用任何风险中性概率测度\(\mathbb{Q}\)从风险中性估价公式计算得出。

  • If a claim X is not attainable then we may define a price of X consistent with the no-arbitrage principle. It can be computed using the risk-neutral valuation formula, but it depends on the choice of a risk-neutral probability measure \(\mathbb{Q}\).
    如果一项索赔 X 无法实现，那么我们可以定义一个符合无套利原则的X价格。它可以使用风险中性估值公式计算，但它取决于风险中性概率测度 \(\mathbb{Q}\) 的选择。

6.1 Proof of FTAP

证明。

[在FTAP中的证明] 我们首先证明“如果”部分。假设..，存在风险中性概率测度Q。

设…是任何初始禀赋为空的交易策略。那么对于任何等式

如果我们假设…，那么最后一个方程意味着等式…必须适用于所有…。

因此，不可能存在满足套利机会所有条件的交易策略。

6.2 Geometric Interpretations

6.2几何解释

• The proof of the implication \((\Rightarrow)\) in the FTAP needs some preparation, since it is based on geometric arguments.
  FTAP中蕴涵\((\Rightarrow)\)的证明需要做一些准备，因为它是基于几何参数的。

• Any random variable on \(\Omega\) can be identified with a vector in \(R^k\) ,specifically,
  \(\Omega\)上的任何随机变量都可以用\(R^k\)中的向量来识别，具体来说，

\[X= (X(\omega_1), . . . ,X(\omega_k))^T = (x_1, . . . , x_k )^T \in R^k .\]

• An arbitrary probability measure Q on W can also be interpreted as a vector in \(R^k\)

\[Q = (Q(\omega_1), . . . ,Q(\omega_k )) = (q_1, . . . , q_k ) \in R^k .\]

• We note that

\[E_Q (X) = \Sigma {i=1}{k} X(\omega_i) Q(\omega_i) = \Sigma_{i=1}^{k}x_i q_i = \langle X,Q \rangle\]

where \(\langle \cdot,\cdot \rangle\) denotes the inner product of two vectors in \(R^k\) .
其中\(\langle \cdot,\cdot \rangle\)表示\(R^k\)中两个向量的内积。

6.3 Axiliary Subsets

轴子集

• We define the following classes:
  我们定义以下类别：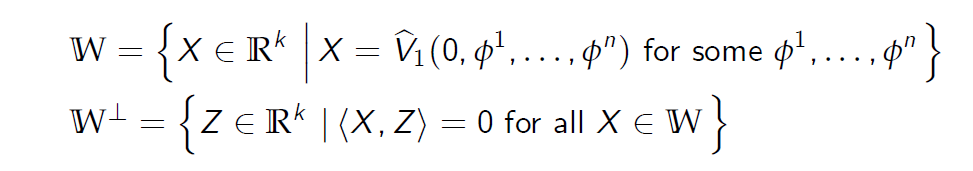

• The set W is the image of the map \(\hat V_1(0,\cdot, . . . , \cdot) : R^n \to R^k \).
  集合W是映射的图像
• We note that W represents all discounted values at t = 1 of trading strategies with null initial endowment.
  我们注意到，W表示初始禀赋为空的交易策略在t=1时的所有贴现值。

• The set \(W^\bot\) is the set of all vectors in \(R^k\) orthogonal to W.
  集合\(W^\bot\)是与W正交的所有向量的集合\(R^k\)。

• We introduce the following sets of k-dimensional vectors:
  我们介绍以下k维向量集：

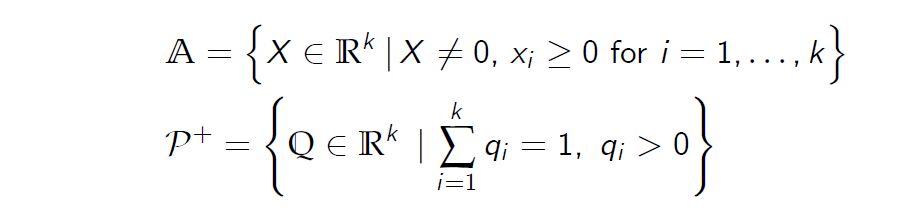
6.4 Vector Spaces

向量空间

推论

W组和\(W ^\perp\)组是\(R^k\)的向量（线性）子空间。

证明。 观察到映射：…是线性的。

换句话说，对于任何交易策略…和…和任意实数…

也是一种交易策略.因此W是\(R^k\)的一个向量子空间。特别地，零向量（0，0，…,0）属于W。

可以直接检验\(W ^\perp\)，即W的正交补也是一个向量子空间。

6.5 Risk-Neutral Probability Measures

6.5 风险中性概率测度

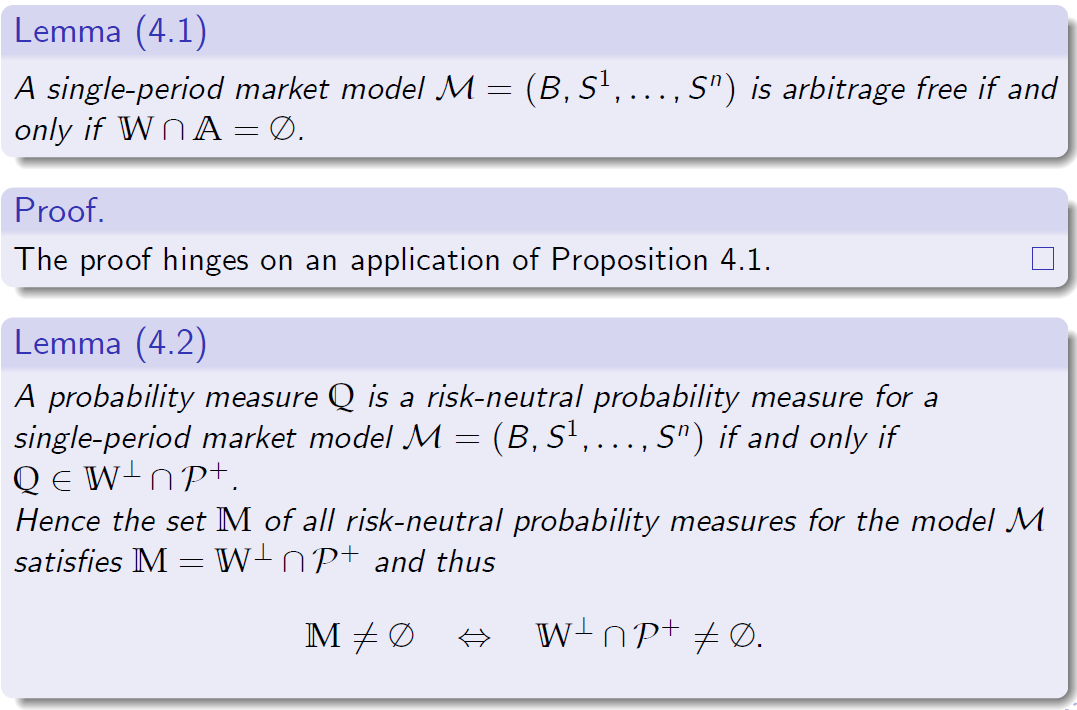
引理（4.1）

单周期市场模型…是无套利的当且仅当…

证明。

证明取决于命题4.1的应用。

引理（4.2）

概率测度Q是单期市场模型M=（B，S1，…）的风险中性概率测度,当且仅当 …

因此，模型扁M的所有风险中性概率测度的集合花M满足…，因此

证明。

在引理4.2中，我们假设Q是风险中性的概率测度。

由性质R.1可知，Q属于P+。

利用R.2性质，我们得到了一个任意向量…

我们的结论是Q也属于\(W ^\perp\)。

因此，Q 按要求显示。

证明。 引理4.2中的证明]我们现在假设Q是W中的任意向量

由于…，我们看到Q是一个满足条件R.1的概率测度

还需要证明Q满足条件R.2。为此，对于x（但任意）j=1，…,n，我们考虑交易策略…

这种交易策略只投资于储蓄账户和jth资产。

该策略的贴现财富为

[引理4.2中的证明（续）]
由于j是任意的，我们看到Q满足条件R.2。
因此Q是一个风险中性的概率度量。
从引理4.1和4.2中，我们得到了FTAP的以下纯几何形式：

From Lemmas 4.1 and 4.2, we get the following purely geometric reformulation of the FTAP:

从引理4.1和4.2中，我们得到了FTAP的以下纯几何形式：

\[\mathbb{W}\ \cap \mathbb{A} = \varnothing \leftrightarrow \mathbb{W}^\bot \cap \mathbb{P}^+ \ne \varnothing .\]

6.6 Separating Hyperplane Theorem: Statement

分离超平面定理：说明

定理（分离超平面定理）

设B，C 是非空的闭凸集，使得 。另外，假设这些集合中至少有一个是紧的（即有界和闭的）。存在向量\(a，y \in R^k\)

证明。

[分离超平面定理的证明]这个证明可以在凸分析或泛函分析的任何教科书中找到。它在课程笔记中概述。

6.7 Separating Hyperplane Theorem: Interpretation

6.7分离超平面定理：解释

• Let the vectors \(a, y \in R^k\) be as in the statement of the Separating Hyperplane Theorem

设向量\(a, y \in R^k\)如分离超平面定理中所述

• It is clear that \(y \in R^k\) is never a zero vector.

很明显，\(y \in R^k\) 永远不是零向量。

• We define the (k - 1)-dimensional hyperplane \(H - R^k \)by setting
  我们定义(k - 1)维超平面\(H - R^k \)记作 \(H= a +\\{x \in R^k | \langle x,y \rangle = 0\\} = a + \\{y\\}^\bot\)

• Then we say that the hyperplane H strictly separates the convex sets B and C.
  然后我们说超平面H严格分离了凸集B和C。

• Intuitively, the sets B and C lie on di¤erent sides of the hyperplane H and thus they can be seen as geometrically separated by H.
  直观地说，集合B和集合C位于超平面H的不同边上，因此它们可以被视为在几何上被H分开。

• Note that the compactness of at least one of the sets is a necessary condition for the strict separation of B and C.
  注意，至少一个集合的紧性是B和C的严格分离的必要条件。

6.8 Separating Hyperplane Theorem: Corollary

6.8分离超平面定理：推论

• The following corollary is a consequence of the separating hyperplane theorem.
  下面的推论是分离超平面定理的结果。

• It is more suitable for our purposes: it will be later applied to B =W and \(C = A^+ := \{X \in A	\langle X,P \rangle =1\} \subset A\).
  它更适合我们的目的：它稍后将应用于B=W和\(C = A^+ := \{X \in A	\langle X,P \rangle =1\} \subset A\)

推论（4.1） 假设B是一个向量子空间，集合C是一个严格凸集，使得B…。存在一个向量y，使得

证明。

[推论4.1的证明：第一步]我们注意到Rk的任何向量子空间都是一个闭的凸集。 从分离超平面定理出发，存在一个，y这样的不等式
对于所有向量b是满足的。由于b是一个向量子空间，对于任何b，向量lb属于b。因此对于任何b2b和l2r，我们有 这又意味着hb，yi=0对于任何向量b2b，意味着y2b。而且，我们有ha，yi>0。

证明。

[推论4.1的证明：第二步]为了建立第二个不等式，

我们观察到，从分离超平面定理，我们得到

We now are ready to establish the implication \((\Rightarrow)\) in the Fundamental Theorem of Asset Pricing, that is,
我们现在已经准备好在基本的\((\Rightarrow)\)资产定价定理，

\[\mathbb{W}\ \cap \mathbb{A} = \varnothing \leftrightarrow \mathbb{W}^\bot \cap \mathbb{P}^+ \ne \varnothing .\]

non-empty非空的 suffices足以 auxiliary set 辅助集 bounded 有界的 convex subset凸子集

Corollary推论

component of Y 是Y的第i个分量

从命题2可以看出，如果一个未定权益X是可实现的，那么期望值

我们用反证法证明了这个推论。因此，让我们假设未定权益X是不可实现的。我们的目标是

考虑第4.4节中引入的矩阵A。

由于权利要求X无法实现，因此没有解决方案

那么B是Rk的一个子空间，显然，集C是凸紧的。

根据推论4.1，存在一个非零向量

其中Aj是矩阵A的第j列。

值得注意的是，向量Y依赖于X。

证明。

[命题证明4.5步骤4]我们假设市场模型是无套利的，因此，

根据FTAP，类M是非空的。

设q2m为任意风险中性概率测度。

我们可以选择一个足够小的实数l>0，以确保每i=1。

下一步，我们的下一个目标是证明bQ也是一个风险中性概率度量，它与Q不同。

在最后一步中，我们将证明不等式（3）是有效的。

还要检查bQ是否也满足条件R.2。

我们研究了股票贴现价格在bQ下的行为

我们得出结论…因此，bQ 2 M，即bQ是市场模型M的风险中性概率测度。

由（5）可知，Q 6=bQ。我们已经证明了这一点

如果M是无套利且不完全的，则存在多个风险中性概率测度。

为了完成证明，还需要证明不等式（3）对于未定权益X是满足的。

回想一下，X是一个固定的不可得未定权益，我们构造了对应于X的风险中性概率测度bQ。

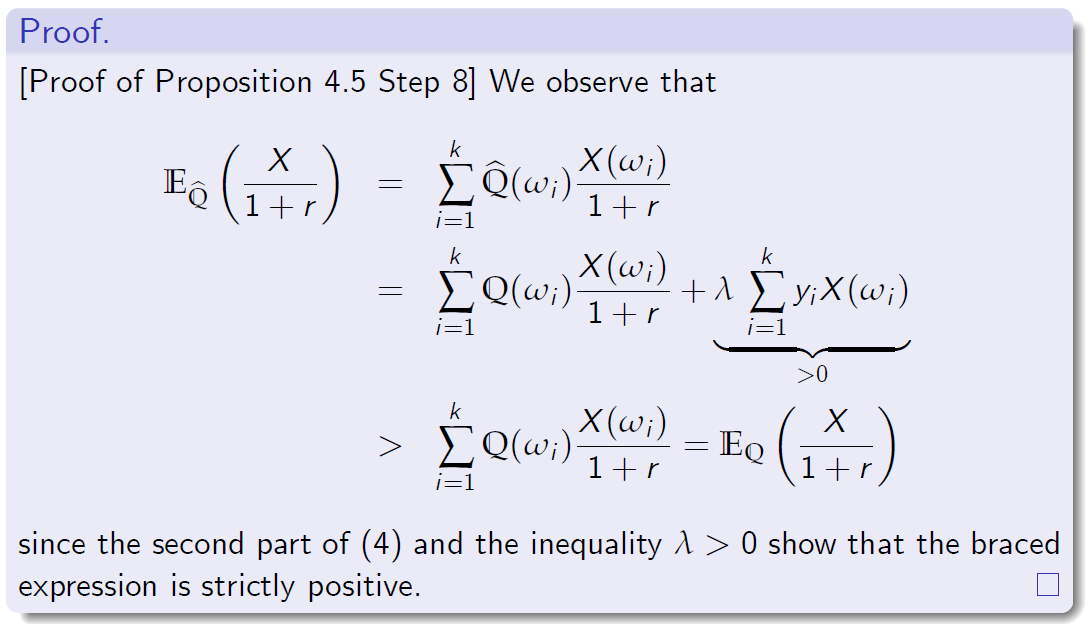
因为（4）的第二部分和不等式l>0证明了带括号的表达式是严格正的。