Unit 4 Filtrations and Conditioning

过滤和调节

Uploaded by eva

1 New Features

新特点

• Two important new features of multi-period market models:
  多期市场模式的两个重要新特点：

  • Investors can trade in assets at any specific time \(t \in \{0,1,2,…,T\}\) where T is the horizon date.
    投资者可以在任何特定时间进行资产交易\(t \in \{0,1,2,…,T\}\)，其中t是水平日期。
  • Investors can gather information over time, since the fluctuations of asset prices can be observed.
    投资者可以随着时间的推移收集信息，因为可以观察到资产价格的波动。
• We have to determine how the level of information evolves over time.
  我们必须确定信息水平是如何随时间发展的。
• The latter aspect leads to the probabilistic concepts of \(\sigma\)-fields and filtrations.
  后一个方面引出了\(\sigma\)-域和过滤的概率概念。

Example

• In one-period model we have the set of possible events (states of nature) \(\Omega = \{\omega_1,\omega_2\}\) at time t = 0, and at time t = 1 we know which state of nature realised. \(\{\omega_1,\omega_2\} = \{‘up’, ‘down’\}\)
  在单周期模型中，我们有一组可能的事件（自然状态）\(\Omega = \{\omega_1,\omega_2\}\)在时间t=0，在时间t=1，我们知道自然状态实现了。\(\{\omega_1,\omega_2\} = \{‘up’, ‘down’\}\)

• In multi-period model the structure of information is more comlex
  在多周期模型中，信息结构更为复杂

  • We start with \(\Omega = A_0 = \{\omega_1, …,\omega_k , …\}\) the set of all possible states of nature.
    我们从\(\Omega = A_0 = \{\omega_1, …,\omega_k , …\}\)自然界所有可能状态的集合开始。

  \((A_0 = \\{'up \ \text{at}\ \ t=1','down \ \text{at}\ \ t=1','up \ \ \ \text{at}\ \ t=2','down \ \text{at}\ \ t=2',...\\}\)

  • at each next period t > 0 we know that some events will never realise,\(A_t \subseteq A_{t-1} \subseteq … \subseteq A_1 \subseteq A_0 \).
    在接下来的每一个时间段t>0，我们知道有些事件将永远不会出现，\(A_t \subseteq A_{t-1} \subseteq … \subseteq A_1 \subseteq A_0 \)。

    （\(\subseteq\) 包含）

  \[(A_1 = \\{'down \ \text{at}\ \ t=1','up \ \ \ \text{at}\ \ t=2',,'down \ \text{at}\ \ t=2',...\\} \subseteq A_0 )\]

So we may denote complement set \(A_t^c = \Omega \ A_t\) which containes all states of nature which are ruled out at time t.
所以我们可以表示补集\(A_t^c = \Omega \ A_t\)，它包含在时间t排除的所有自然状态。

Example 5.4: Stock Price Model

5.4： 股票价格模型

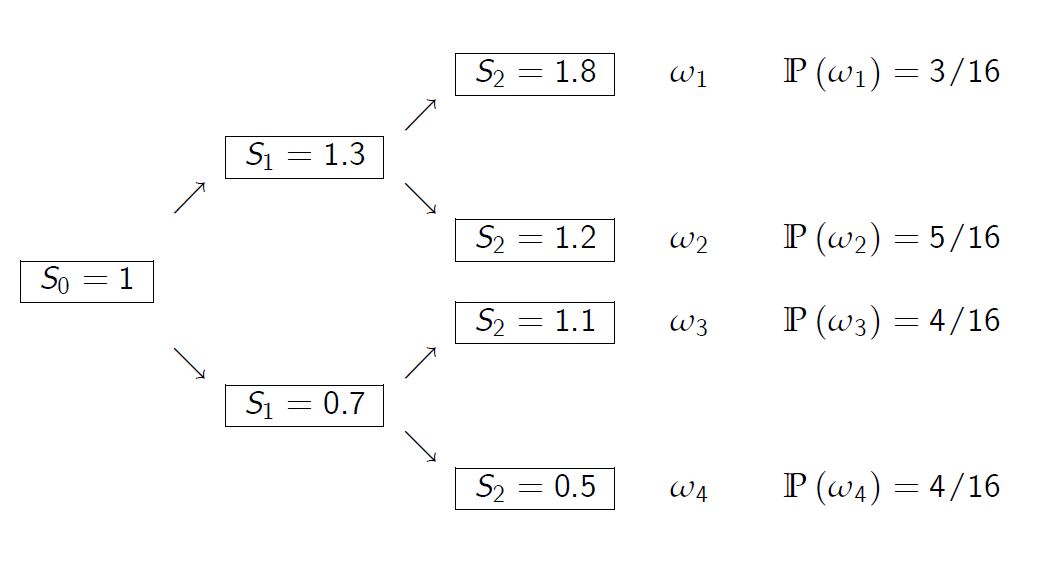
Example: Stock Price Model

示例（5.4续）

• 在时间零点，投资者观察到\(S_0=1\)，对真实的未来状态没有任何线索，所以\(\cal F_0 =\{\emptyset,\Omega\}\)
• 在t=2时，投资者观察 \(S_2\) 并知道实数集 \(\omega\)。 \(\cal F_2=2^{\Omega}\)，因为生成 \(\cal F_2\) 的分区是

• 在t=1时，投资者观察到 \(S_1=1.3\) 或 \(S_1=0.7\)，因此它不是\(\{\omega_1,\omega_2\}\)就是\(\{\omega_3,\omega_4\}\)。相关分区为

• 注意\(\emptyset,\Omega\)必须始终存在，因为\(\Omega\)是所有可能性集合的并集，并且 \(\emptyset\) 是‘zero’并且是 \(\Omega\) 的补集。换句话说，\(\cal F\)不是一个代数/域。

例子（5.4 连续）

• 价格流程同上
• 在时间t=1时，进行市场调查，调查结果为有利的\(\{\omega_1,\omega_2\}\)或不利的\(\{\omega_3,\omega_4\}\).
• 此外，在任何一种情况下，风险证券都可能采用一个或两个离散值。因此，时间t=1的相关分区为
• 投资者可以在时间1区分\(\omega_1\)从\(\omega_2\)以及\(\omega_3\)从\(\omega_4\)。
• 他们可以展望未来，因为他们知道 t=2 时的价格是多少。
• 在这种情况下，信息流是不同的，尽管价格过程是相同的。

1.Partitions and \(\sigma\)-Fields

1.区分和 \(\sigma\)-域

1.1 \(\sigma\)-Fields

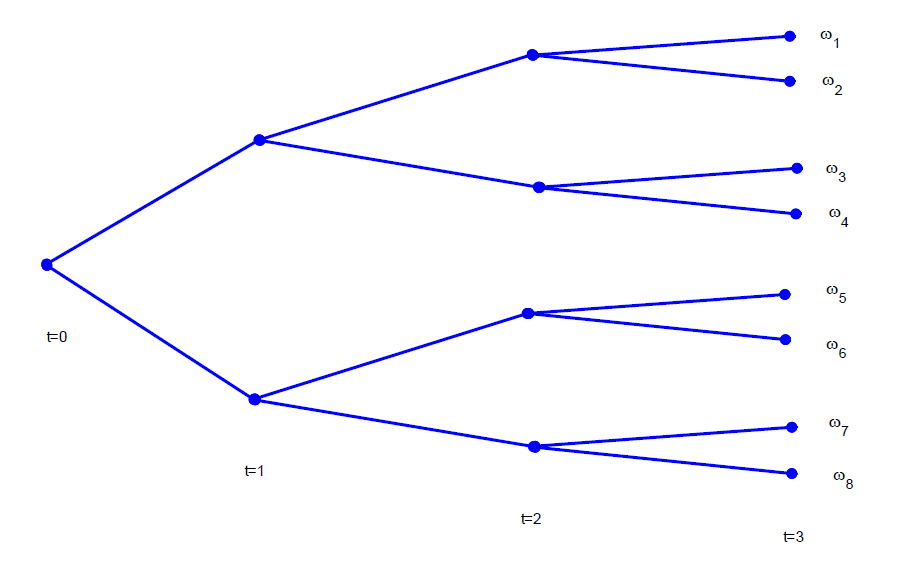
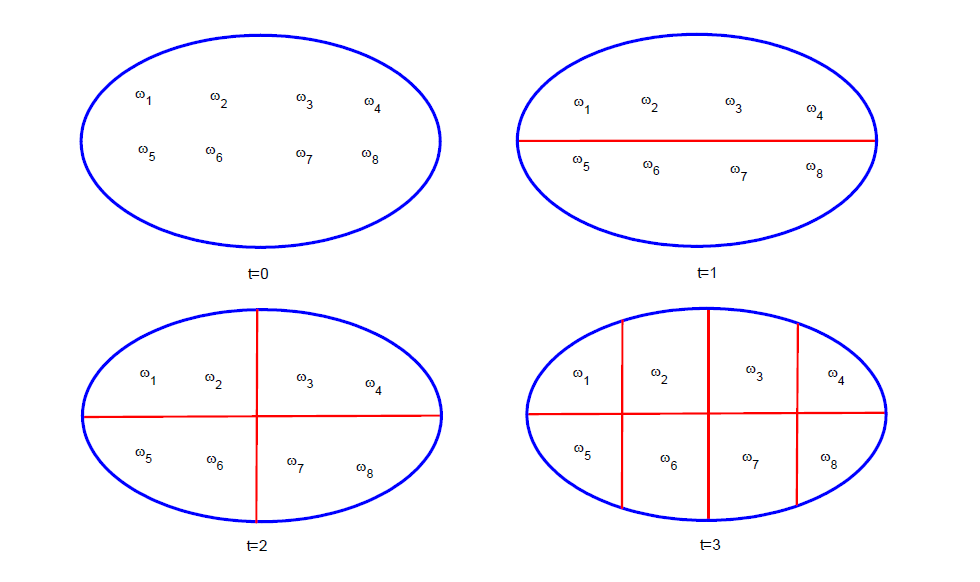
• The model of information structure can be described using sequence of partitons, where each partition becomes finer. Or it can be described using trees.
  信息结构模型可以用分部序列来描述，其中每个分部变得更细。也可以用树来描述。

• The concept of a \(\sigma\)- field can be used to describe the amount of information available at a given moment.
  \(\sigma\)- field的概念可用于描述给定时刻可用的信息量。

• Let \(N = \{1, 2, …\}\) be the set of all natural numbers.
  设\(N = \{1, 2, …\}\)是所有自然数的集合。

\(\Omega\)的子集的集合 \(\cal F\) 称为 \(\sigma\)-域（或\(\sigma\)-代数）

• It follows that the empty set belongs to \(\cal F:\varnothing = \Omega^c \in \cal F\)
  因此，空集属于\(\cal F:\varnothing = \Omega^c \in \cal F\)

• So, we have defined algebra: zero element is there, the inverse element is there, and an operation is defined.
  所以，我们定义了代数：零元素在那里，逆元素在那里，定义了一个运算。

• Moreover, it is a field as two operations (sum=union and multiplication=intersection) are defined, existence of inverse operation. Most of the literature uses \(‘\sigma-algebra’\)rather than \(\sigma\)-field.
  此外，当定义了两个运算（和=并，乘=交）时，它是一个域，存在逆运算。大多数文献使用\(‘\sigma-algebra’\)而不是\(\sigma\)-域。

1.2 Interpretation of a \(\sigma\)-Fields

\(\sigma\)-Fields的解释

• Many different \(\sigma\)-Fields can be defined on one set \(\Omega\).
  可以在一个集合\(\Omega\)上定义许多不同的\(\sigma\)-Fields

• The set of information has to contain all possible states, so that we postulate that \(\Omega\) belongs to each \(\sigma\)-Fields.
  信息集必须包含所有可能的状态，因此我们假设\(\Omega\)属于每个\(\sigma\)-Fields。

• Any set \(A \in \cal F\) is interpreted as an observed event.
  任何集合\(A \in \cal F\)都被解释为观察到的事件。
• If an event \(A \in \cal F\) is given, that is, some collection of states is given, then the remaining states can also be identified and thus the complement \(A^c\) is also an event.
  如果给定了一个事件\(A \in \cal F\)，也就是说，给定了一些状态集合，那么剩余的状态也可以被识别，因此补集\(A^c\)也是一个事件。

• The idea of a \(\sigma\)-Fields is to model a certain level of information.
  \(\sigma\)-Fields的概念是对一定级别的信息进行建模。

• We will later introduce a concept of an increasing flow of information, formally represented by an ordered family of \(\sigma\)-Fields.
  我们稍后将介绍一个信息流不断增加的概念，正式表示为\(\sigma\)-域的有序族。

1.3 Probability Measure

定义（概率测度） 映射\(\mathbb P : \cal F \to \) [0，1]被称为概率度量，如果
对于任意序列 \(A_i，i \in \mathbb N\) 的互斥事件
这三项\((\Omega，\cal F，\mathbb P)\) 称为概率空间。

• Note that \(\mathbb P(\varnothing) = 0 \) due to the definition of probability measure.
  注意，\(\mathbb P(\varnothing) = 0 \)是由于概率测度的定义。
• By convention, the probability of all possibilities is 1.
  按照惯例，所有可能性的概率都是1。
• Probability should satisfy \(\sigma\)-additivity.
  概率应满足\(\sigma\)-可叠加性。

1.4 Example: \(\sigma\)-Fields

subsets 子集

\(\cal F_1\) : 没有信息，除了设置 \(\Omega\)
\(\cal F_2\) : 部分信息，因为我们无法区分 \(\omega_1\) 或 \(\omega_2\) 的出现。
\(\cal F_3\) : 完整信息，因为可以观察到事件\(\{\omega_1\}\)、\(\{\omega_2\}\)、\(\{\omega_3\}\)和\(\{\omega_4\}\)。

1.5 Example: Probability Measure

additivity 叠加性

• 注意，\(\mathbb P\) 在 \(\sigma\)-Fields \(\cal F_3 = 2^\Omega\) 上还没有定义，事实上 \(\mathbb P\)从\(\cal F_2\) 到 \(\cal F_3\) 的扩展不是唯一的。

1.6 Partitions

1.6 分隔

定义
设 I 是某个指标集。假设我们得到了 \(\Omega\) 的子集的集合
\((B_i){i\in I}\) 那么包含该集合的最小 \(\sigma\)-Fields 用 \(B_i{i \in I}\) 表示，并称为集合\((B_i)_{i\in I}\) 生成的\(\sigma\)-Field。

定义 （分隔）

通过 \(\Omega\) 的划分，我们指的是\(\Omega\)的非空子集的任何集合 \(\cal P=（ A_i )_{i \in I}\)，使得集合 \(A_i\) 互斥，即，

引理
分区\(\cal P=（ A_i )_{i \in I}\) 生成一个 \(\sigma\)-Fields，如果每个集合 \(A \in F\) 都可以写成某些 \(A_is\) 的并集，即

1.7 Partition Associated with a \(\sigma\)-Field

分隔与\(\sigma\)-Field的区别

定义（与\(\cal F\) 相关的分区）

与\(\sigma\)-Field 相关联的 \(\Omega\) 的一个分区是一些 \(i \in I\) 的非空集\(A_i \in \cal F\)的集合，使得

引理 对于\(\sigma\)-Field 状态空间 \(\Omega\) 的子集的任何 \(\sigma\)-Field，与该 \(\sigma\)-Field 相关联的分区总是存在且是唯一的。

Further properties of partitions:
分区的其他属性：

• If \(\Omega\) is countable then for any \(\sigma\)-Fields F there exists a unique partition P of \(\Omega\) associated with F. It is also clear that this partition generates F, so that \(\cal F = \sigma(P)\)
  如果 \(\Omega\) 是可数，那么对于任何\(\sigma\)-Fields F，存在一个与\(\cal F\)相关联的\(\Omega\)的唯一分区P。很明显，这个分区生成F，因此\(\cal F = \sigma(P)\)

• The sets \(A_i\) in a partition must be smallest, specifically, if \(\cal F = \sigma(P)\) and \(A \in F\) is such that \(A A_i \)then \(A = A_i\) .
  分区中的集合\(A_i\)必须是最小的，具体来说，如果\(\cal F = \sigma(P)\)和\(A \in F\)中的\(A A_i \)是这样的，那么\(A = A_i\)。
• The probability of any \(A \in \cal F\) equals the sum of probabilities of \(A_{iS}\) in the partition generating F, specifically,
  F中任意\(A \in \cal F\)的概率等于生成F的分区中\(A_{iS}\)的概率之和，具体地说，

\[A = \bigcup_ {i \in j} A_i \Rightarrow P(A)= \Sigma_{i \in J} P (A_i)\]

1.8 Example: Partition Associated with a \(\sigma\)-Field

1.9 Random Variable and Measurability

Let \(\cal F\) be an arbitrary \(\sigma\)-Field of subsets of \(\Omega\). In the next definition, we do not assume that the sample space is discrete.
设F是W的子集的任意\(\sigma\)-域。在下一个定义中，我们不假设样本空间是离散的。

定义（\(\cal F\)-可测量性）

映射 X: \(\Omega\ \to \mathbb R \) 如果函数 \(\omega \to X（\omega）\)在与 \(\cal F\) 对应的分隔中的任何子集上是常数。等价地，对于每个实数 X 的子集\(\{\omega \in \Omega : X（\omega）=x\}\) 是代数\(\cal F\) 的一个元素。

如果 X 是\(\cal F\)-可测的，那么X称为\(（\Omega，\cal F）\)上的随机变量。

Example

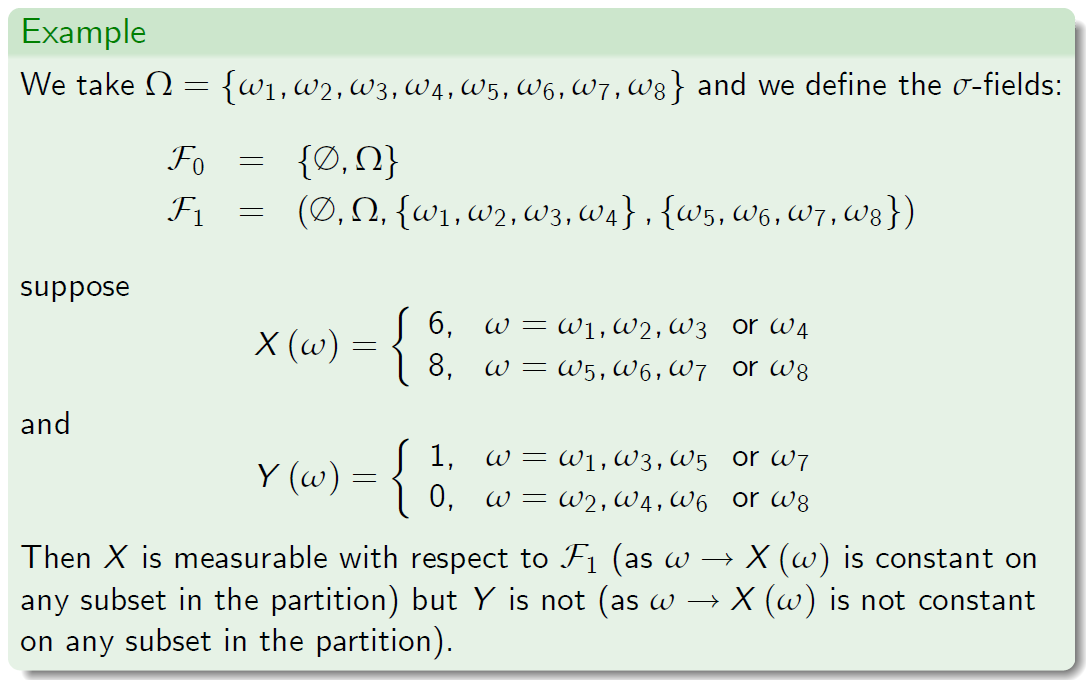
那么X相对于F1是可测量的（如w！X（w）在分区中的任何子集上都是常量，但Y不是常量（如w！X（w）在分区中的任何子集上都不是常数。

1.10 Information Flow: Filtration

1.10信息流：过滤

• In a typical application, the information about random events increases over time.
  在典型的应用程序中，有关随机事件的信息会随着时间的推移而增加。

• To model the information flow, we introduce the concept of a filtration.
  为了对信息流进行建模，我们引入了过滤的概念。

• The following definition covers the cases of the discrete and continuous time.
  以下定义涵盖了离散时间和连续时间的情况。

\(\Omega\) 上 \(\sigma\)-Fields的族（\(\cal F_t)_{0 \leq t \leq T}\) 称为过滤，如果\(\cal F_s \subset F_t\) 每当 \(s \leq t\)，为简洁起见，我们表示 \(F =（\cal F_t）0 \leq t \leq T\) 。

• We interpret the \(\sigma\)-Field \(F_t\) as the information available to an agent at time t. In particular, \(F_0\) represents the information available at time 0, that is, the initial information.

我们将\(\sigma\)-Field \(F_t\)解释为代理在时间t可用的信息。特别是，\(F_0\)表示在时间0可用的信息，即初始信息。

• We assume that the information accumulated over time can only grow, so that we never forget anything!
  我们假设随着时间积累的信息只能增长，这样我们就永远不会忘记任何事情！

2.Filtrations and Adapted Stochastic Processes

2.过滤和适应的随机过程

2.1 Stochastic Process

2.1随机过程

定义（随机过程） 随机过程是实值函数
对于每个固定的…函数…称为采样路径。对于每个固定 t，函数…是一个随机变量。如果每t=0，1。，T 随机变量 Xt 是Ft可测的。

例子（5.3） 再考虑一下基本市场模型。股票价格在W=fw1，w2g上的随机过程为S0和S1，过滤函数为为F0=fÆ，Wg和

注意F0是初始信息，这意味着投资者只知道所有可能的状态。

Example 5.4: Stock Price Model

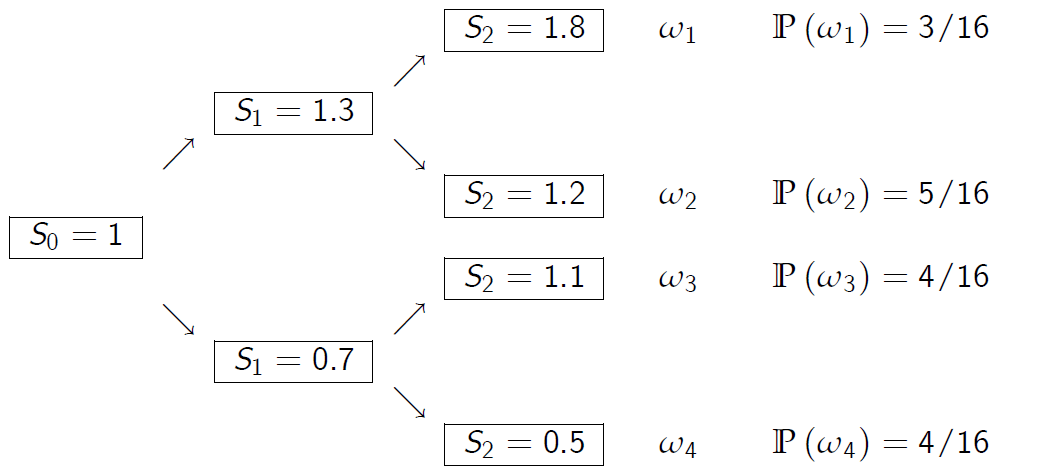
例如：股票价格模型

示例（5.4续）

• 在时间零点，投资者观察到S0=1，对真实状态没有任何线索，因此F0=。
• 在t=2时，投资者观察S2并知道真实状态w.F2=2W，因为生成F2的分区是
• 当t=1时，投资者观察到S1=1.3或S1=0.7，因此
• 注意，\(\emptyset，\Omega\)必须始终存在，因为W是所有可能集合的并集，而Æ是“零”并且是W的补码。换句话说，F不是代数/域。
• 注意，随机过程 \(S_n\) 适用于过滤。

2.2 Filtration Generated by a Stochastic Process

2.2随机过程产生的过滤

• A filtration construced in previous example is said to be generated by the stochastic process.
  前一示例中构造的过滤被称为由随机过程生成。

• It is the coarsest one possible, i.e. the various algebras have the fewest possible subsets such that the stochastic process under discussion is adapted.
  它是可能的最粗糙的一个，即各种代数具有尽可能少的子集，这样所讨论的随机过程就适应了。

• Notation: Let \(X=(X_t)_{0 \le t \le T}\) be a stochastic process on the probability space \((\Omega,F,P)\).

记法：设\(X=(X_t)_{0 \le t \le T}\)是概率空间\((\Omega,F,P)\)上的随机过程。

\(F^X = (F_t^X)\) \(0 \le t \le T\)is the filtration generated by the process X.
是由进程X生成的过滤。

• But there is another way to construct the securities market model, see the next slide.
  但构建证券市场模型还有另一种方法，见下一张幻灯片。

Example: Stock Price Model

例如：股票价格模型

示例（5.4续）

价格流程同上

在时间t=1时，进行市场调查，调查结果为有利的fw1、w2g或不利的fw3、w4g

此外，在任何一种情况下，风险证券都可能采用一个或两个离散值。因此，时间t=1的相关分区为

投资者可以在时间1区分w1和w2以及w3和w4。

他们可以展望未来，因为他们知道t=2时的价格是多少。

在这种情况下，信息流是不同的，尽管价格过程是相同的。

3.Conditional Expectations

3.条件期望

3.1 Conditional Expectation in Elementary Probability Theory

3.1初等概率论中的条件期望

Sample space \(\Omega\) is finite.
样本空间\(\Omega\)是有限的。

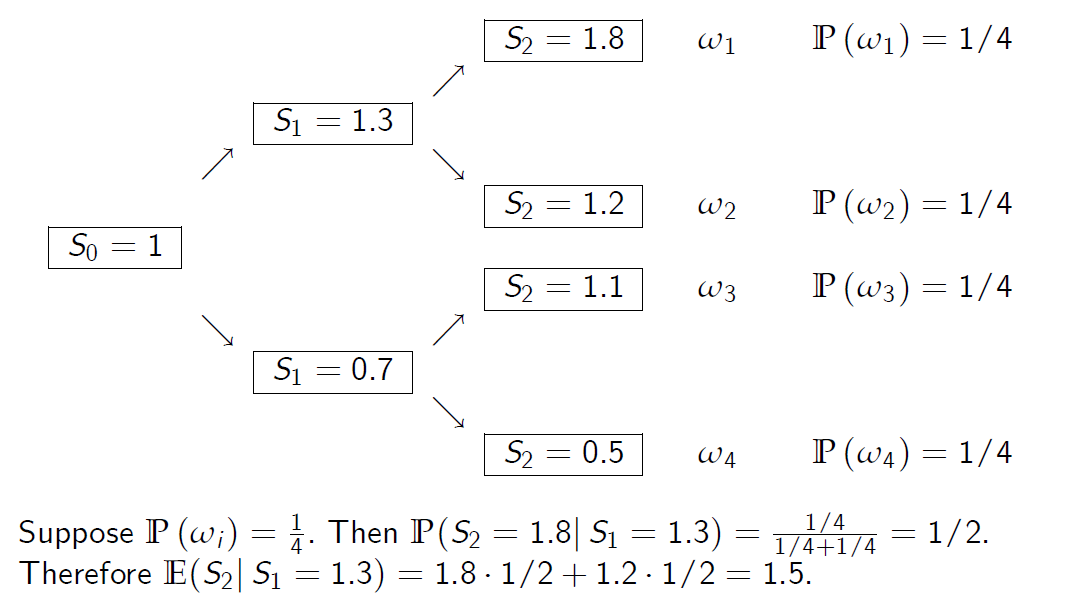
定义

给定事件A的离散随机变量X的条件期望表示为E，并用条件概率分布P定义为

3.2 Conditional Expectations

3.2条件期望

• Let \((\Omega,\cal F,\mathbb P)\) be a finite (or countable) probability space.
  设\((\Omega,F,P)\)为有限（或可数）概率空间。
• Let X be an arbitrary F-measurable random variable.
  设X为任意F-可测随机变量。
• Assume that G is a s-field which is contained in F.
  假设G是包含在F中的s域。
• Let \((A_i ){i \in I}\) be the unique partition associated with G.
  设\((A_i ){i \in I}\)是与G相关联的唯一分区。

• Our next goal is to define the conditional expectation \(E_P(X	G)\),that is, the conditional expectation of a random variable X with respect to a \(\sigma\)-Field G.
  我们的下一个目标是定义条件期望\(E_P(X	G)\)，即随机变量X相对于\(\sigma\)-域G的条件期望。

We work with stochastic processes defined on a filtered probability space need to define \(E_P(X| G)\). It is convenient to use \(E_P(X| G)\) as a sum of all conditional expectations of the form \(E_P(X| A)\) as the event A runs through the algebra G.
我们研究定义在过滤概率空间上的随机过程，需要定义\(E_P(X| G)\)。当事件a通过代数G时，使用\(E_P(X| G)\)作为\(E_P(X| A)\)形式的所有条件期望的总和是很方便的。 We can see that
我们看得出来

\[E_p(X|G) 1_A = E_p (X|A) for \ all \ A \in P\]

where P is partition of \(\Omega\) that corresponds to G.
其中P是与G相对应的\(\Omega\)的分区。

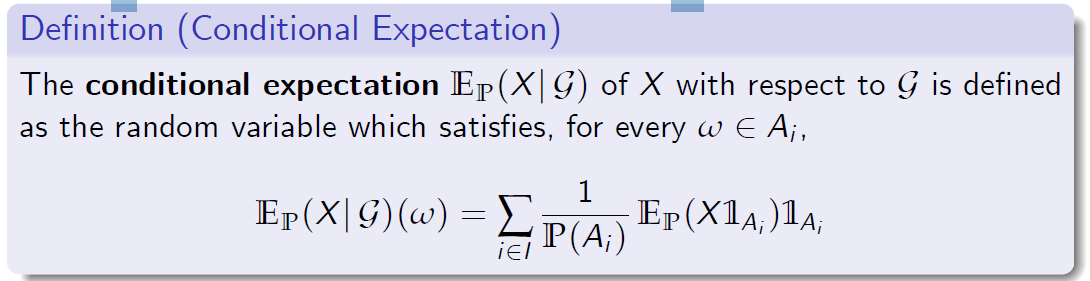
定义（条件期望）

X对G的条件期望EP（X G）被定义为随机变量，对于每个 \(\omega \in A_i\) ，

This generalises the definition of conditional expectation to probability spaces when \(\Omega\) is not finite.
当\(\Omega\)不是有限时，这将条件期望的定义推广到概率空间。

Properties of Conditional Expectation
条件期望的性质

• E_P(X

  G) is G-measurable random variable 是G-可测随机变量

• E_P(X

  G) is the best estimate of X given the information represented by the \(\sigma\)-Field G. 是给定由\(\sigma\)-字段G表示的信息的X的最佳估计。

• The following identity uniquely characterises the conditional expectation (in addition to G-measurability): 以下恒等式唯一地描述了条件期望（除了G-可测性）：

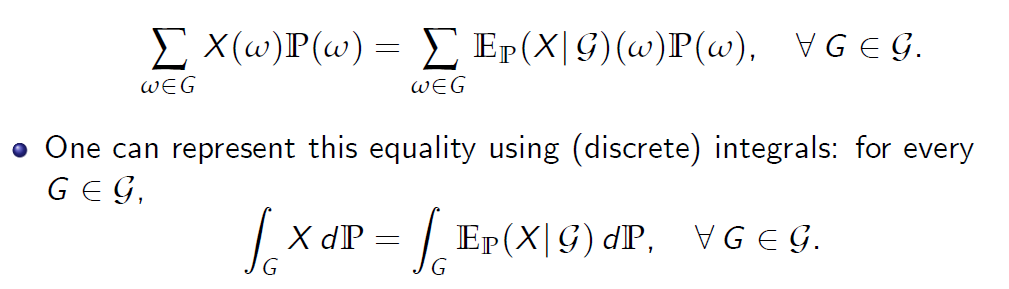
我们可以用（离散）积分来表示这个等式：对于每个

设（W，F，P）被赋予替代 \(\sigma\)-Field \(\cal G\) 和F的 \(\cal G_1 \subset \cal G_2\)， 。然后
1塔属性：如果X 是F-可测的随机变量，那么 2取出已知的：如果X 是G-可测随机变量，Y:W！R是F-可测的随机变量，那么 3琐碎的条件作用：如果X:W！R是一个F-可测的随机变量，与G无关

Example 5.5: Conditional Expectation

例5.5：条件期望

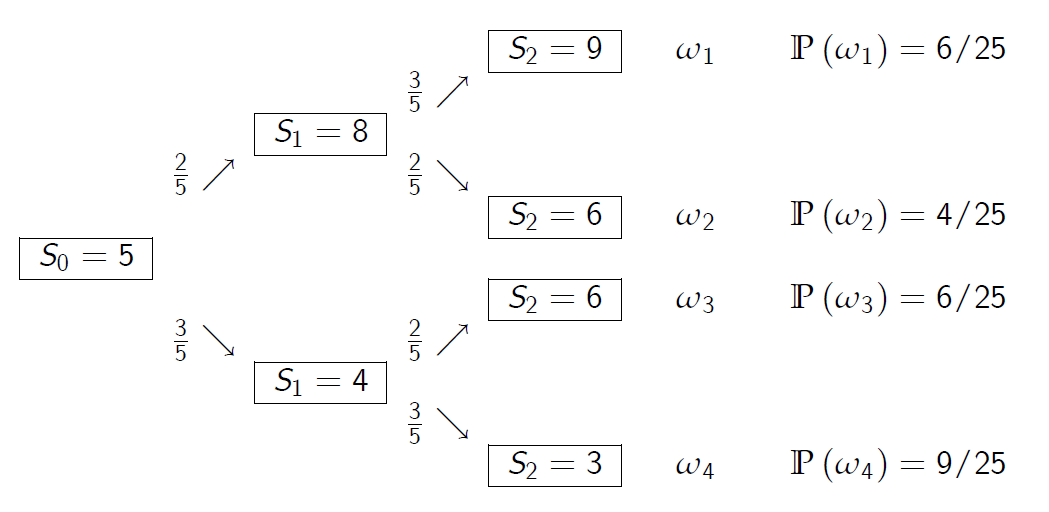
Example: Conditional Expectation

示例（5.5）

基本概率空间由 W= 给出。

在时间t=0时，股票价格已知，唯一值为S0=5。

因此 s场FS

0是平凡的s域。

在时间t=1时，库存可以取两个可能的值，以便

4.Change of a Probability Measure

4.概率测度的变化

4.1 Change of a Probability Measure

4.1概率测度的变化

• Let P and Q be equivalent probability measures on \((\Omega,F)\).
  设P和Q是\((\Omega,F)\)上的等价概率测度。
• Let the density of Q with respect to P be 设Q相对于P的密度为

\[\frac {d Q}{d P} (\omega) = L (\omega)\]

meaning that L is F-measurable and, for every \(A \in F\),

意味着L是F-可测的，并且对于每一个\(A \in F\)

\[\int_{A} X dQ = \int_{A} XL\ dP\]

• If \(\Omega\) is finite then this equality becomes
  如果\(\Omega\)是有限的，那么这个等式变成 \(\Sigma_{\omega \in A} X(\omega) Q(\omega)= \Sigma_{\omega \in A} X(\omega) L(\omega) P(\omega)\)

• Random variable L is strictly positive and \(E_P(L) = 1\).
  随机变量L是严格正的且\(E_P(L) = 1\)
• Equality \(E_Q(X) = E_P(XL)\) holds for any Q-integrable random variable X (it suffices to take A = \(\Omega\)).
  等式\(E_Q(X) = E_P(XL)\)适用于任何Q-可积随机变量X（取A=A = \(\Omega\))）。

4.2 Abstract Bayes formula

4.3 Martingales

4.3 鞅

Martingales are stochastic processes representing fair games.
鞅是代表公平博弈的随机过程。

鞅

鞅是表示公平博弈的随机过程。

定义（鞅）

有限概率空间上的F-适应过程\(X=(X_t)_{0 \le t \le T}\)

（W，F，P）称为鞅

要建立上述等式，必须检查每个

定义

在有限概率空间（W，F，P）上的F-适应过程\(X=(X_t)_{0 \le t \le T}\)称为一个超鞅

有限概率空间（W，F，P）上的F适应过程\(X=(X_t)_{0 \le t \le T}\)称为子鞅