Unit 8 Greeks, Hedging and limits of Black-Scholes

Uploaded by eva

Black-Scholes formula

The Black-Scholes option valuation formula

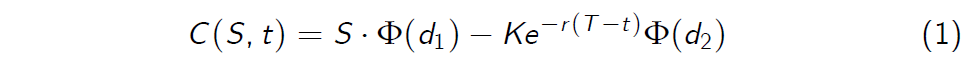
where \(\Phi(x)\) denotes the distribution function of the standard normal distribution, i.e.

for \(x \in \mathbb R\) and

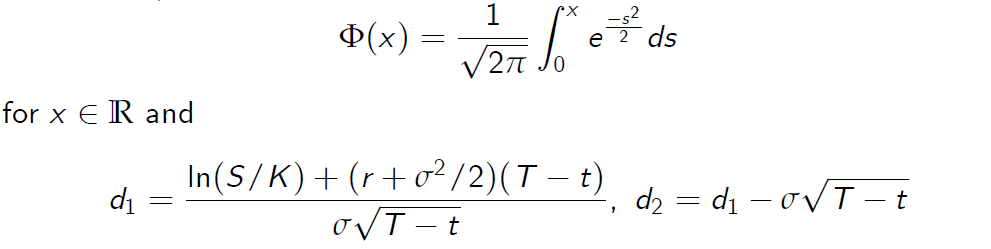
obviously depends on the parameters S,t,K,r and \(\sigma\).

The Black-Scholes Model

• In the Black-Scholes model, one needs to know the five parameters to price European call or put options:

  • The interest rate r .
  • The current stock price \(S_t\) .
  • The strike price K.
  • The time to maturity T - t.
  • \(\sigma\)
• Apart from s, it is easy to observe the other four parameters.
• How to estimate the volatility parameter \(\sigma\) ?

Proposition (5.4)

Suppose that the stock price satisfies the Black-Scholes assumption, i.e., equation (1). Then under the risk neutral probability measure \(\mathbb Q\), we have

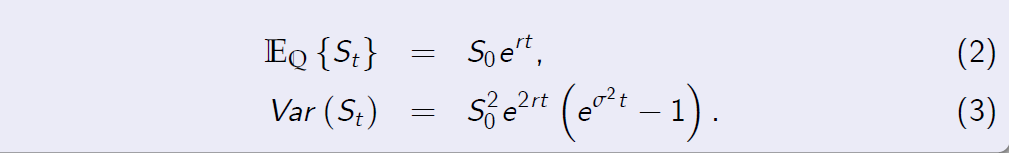
Proof.

[Proof of Proposition 5.4] By Proposition 5.2, ˆSt is a martingale and thus

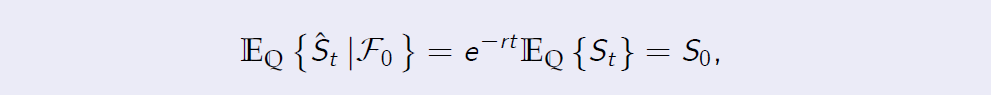
which leads to equation (9).

Proof. [Proof of Proposition 5.4] Furthermore,

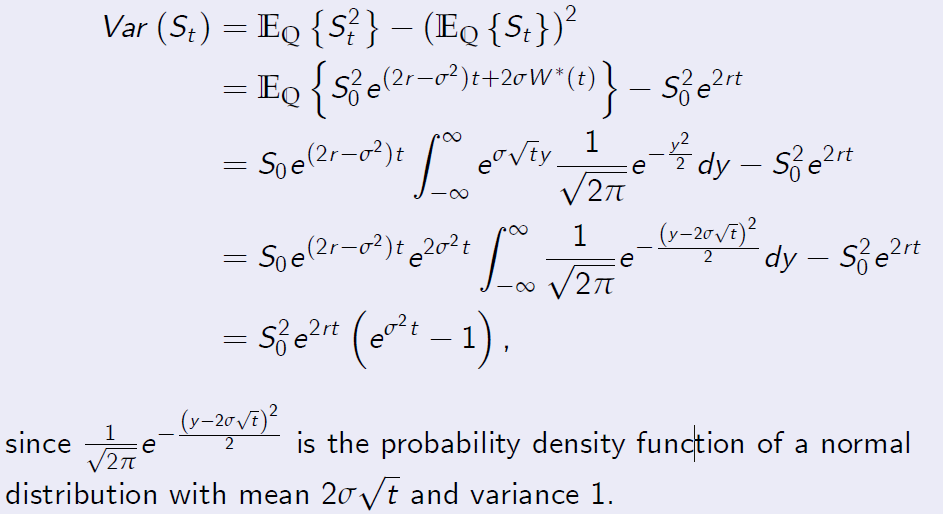
sine \(\frac {1}{\sqrt{2 \pi}} e^{-\frac {(y-2\sigma\sqrt{t})^2}{2}}\) is the probability density function of a normal distribution with mean \(2\sigma\sqrt{t}\) and variance 1.

• Two ideas to estimate s in the Black-Scholes model:
  • Idea 1.: Collect some historical stock prices to evaluate the variance \(\cal v\) and then apply equation (10):

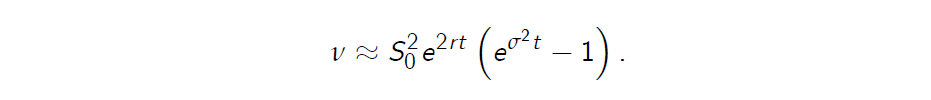
• Idea 2.: Collect some historical stock prices per \(\Delta t, S_0, S_{\Delta t} , . . . , S_{N \Delta t}\) ,and define the return R, where \(R_t =\frac {S_{t+\Delta t}-S_t}{S_t}\), for \(t = 0, . . . , (N - 1) \Delta t\). Then compute the variance of R and

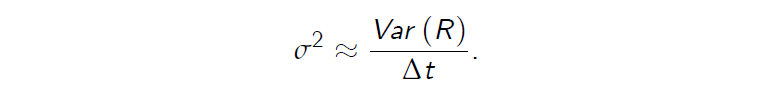
The Black-Scholes Model

• Since \(dlnS_t \approx lnS_{t+\Delta t} - lnS_t\) and

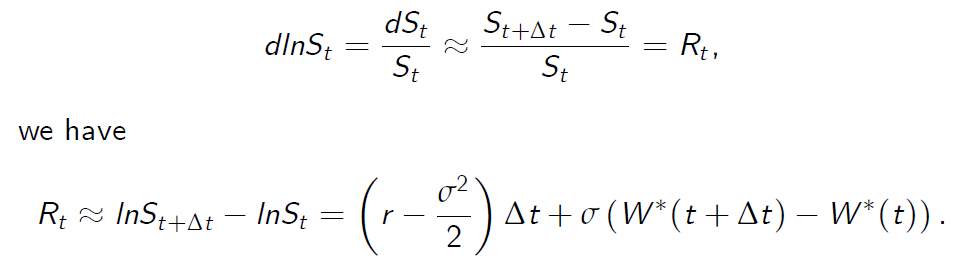
Then \(Var (R) = \sigma^2 \Delta t\), which leads to Idea 2.

The Black-Scholes Model

Example (5.1)

Consider a contingent claim X which pays a payo¤ of twice stock price at the maturity date T. Let the payo¤ function of X be denoted by h (S) = 2S. The price of X at t given the current stock price \(S_t = x\) is, by equation (5),

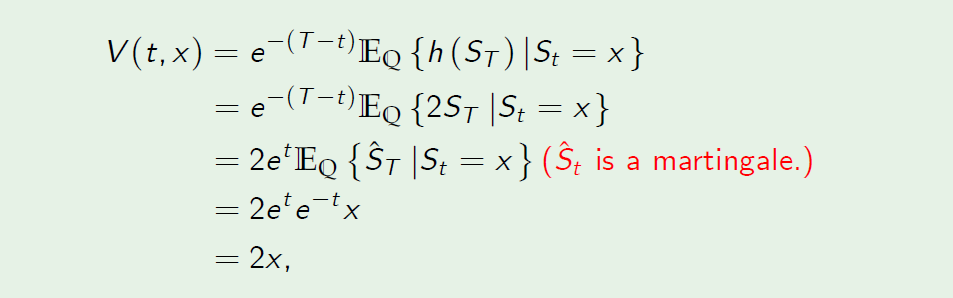
which leads to the price of X at t is twice the current stock price.

Example (5.2)

Consider the same problem in Example 5.1, the Black-Scholes equation for the contingent claim X is given by

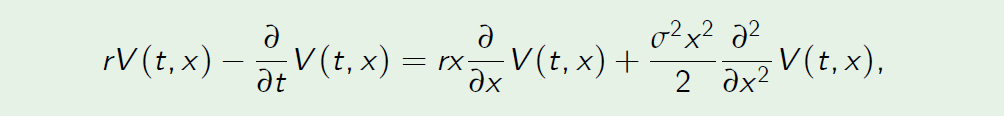
with the boundary condition V (T, x) = 2x. We guess that the closed form solution is given by V (t, x) = A(t)x. Substituting V (t, x) = A(t)x into the Black-Scholes equation gives

\[A'(t)=0\]

which leads A(t) to be a constant. Moreover, V (T, x) = 2x = A(T)x.
Then A(t) = A(T) = 2 and V (t, x) = A(t)x = 2x, which is consistent with the result in Example 5.1.

• The Black-Scholes formula, equation (7) and (8), has been widely used in practice. However, most derivatives do not have closed-form pricing formulas, since neither equation (5) nor the Black-Scholes equation can be solved analytically, in general.

• Numerical methods are important in mathematical finance:

  • Equation (5): The Monte Carlo scheme.
  • Bellman equations: The finite difference methods, the Markov chain approach, or the projection methods.

Overview

In this lecture we derive the expressions for the partial derivatives of the option price with respect to these quantities.
These results are useful for a number of reasons :

1. Traders like to know the sensitivity of the option value to changes in these quantities. The sensitivities can be measured by these partial derivatives.
2. Examining the signs of the derivatives gives insight into the underlying formulas.
3. The derivative \(\Delta = \frac {\partial C}{\partial S}\) is needed for hedging a contingent claim \(\Rightarrow\) Delta-hedging.
4. The derivative \(\Delta = \frac {\partial C}{\partial S}\) can be used to compute implied volatilities.

Greeks

We first focus on the case of a European call option whose price we denote with C(t, S,T,K).
Certain partial derivatives of option prices are so widely used that they have been assigned Greek names and symbols :

1. \(\Delta := \frac {\partial C}{\partial S}\) the “Delta”
2. \(\Gamma := \frac {\partial^2 C}{\partial S^2}\) the “Gamma”
3. \(\rho := \frac {\partial C}{\partial r}\) the “Rho”
4. \(\Theta := \frac {\partial C}{\partial t}\) the “Theta”
5. \(vega := \frac {\partial C}{\partial \sigma}\) the “Vega”

Note that vega is not actually a Greek letter.

Greeks

By differentiating equation (1) with respect to the corresponding equations one can obtain explicit expressions for the Greeks.
The computations are however a little bit messy. We illustrate these computations at the example of \(\Delta\),\(\Gamma\) and \(\rho\). The others follow similarly.
First it follows from the definition of the Distribution function \(\Phi(x)\) that

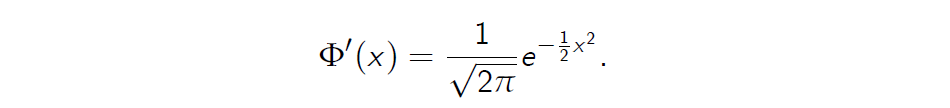
Furthermore it can be shown that

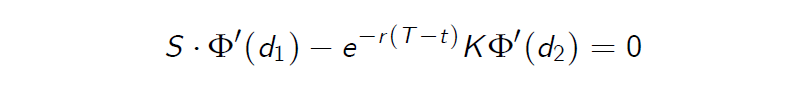
Greeks
Differentiating the BS-formula (1) with respect to S therefore leads to

Taking another derivative with respect to S gives the G :

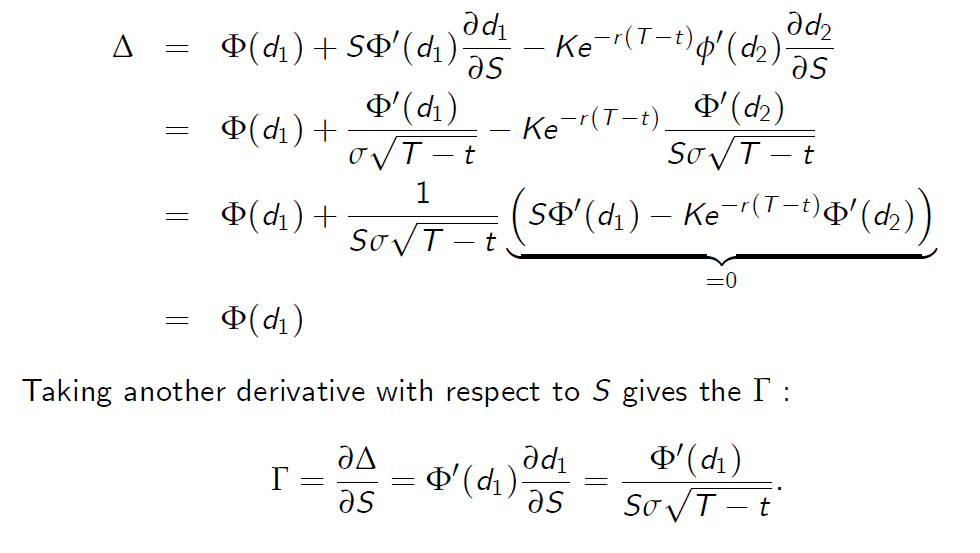
Greeks

Next let us differentiate C with respect to r in order to obtain the \(\rho\):

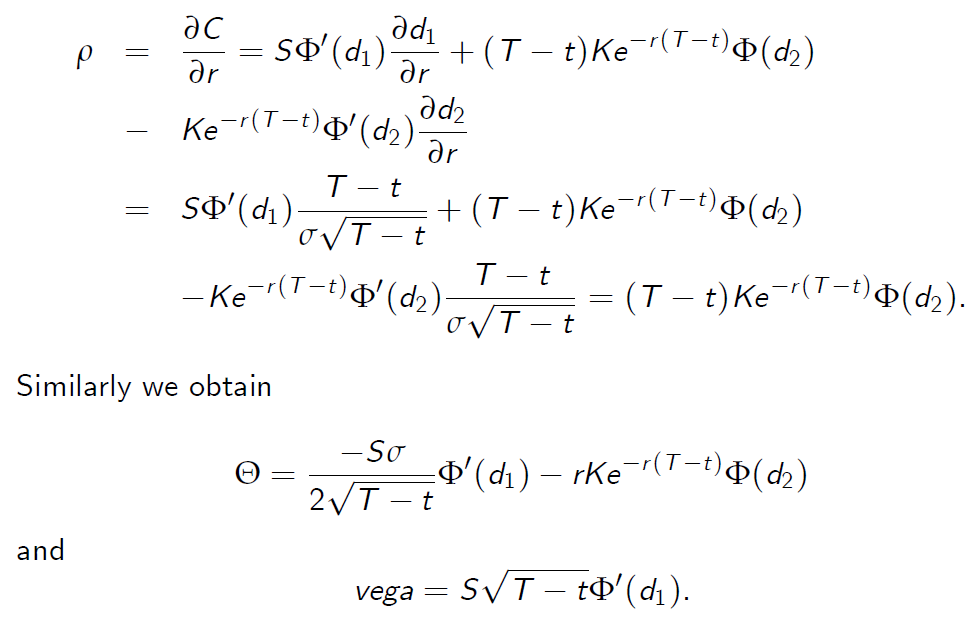
Greeks
The following proposition summarizes the results about the Greeks:

Proposition

Let C(t, S,T,K) denote the price of a European call option in the standard Black Scholes model. Then the Greeks are given by the following expressions :

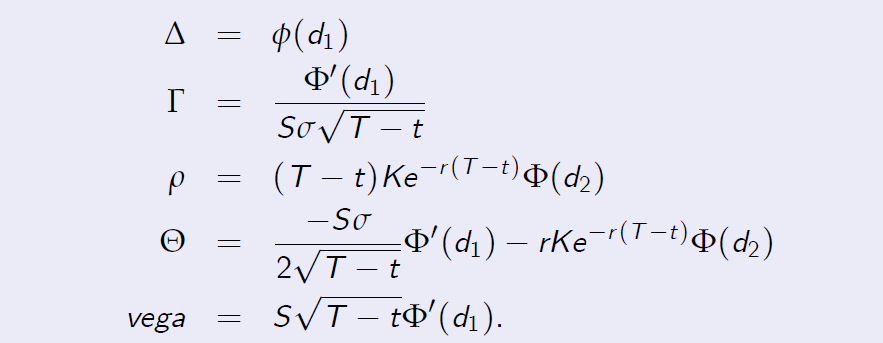
Greeks
The expression for the Delta also follows from the following consideration:
We know from the derivation of the Black Scholes partial differential equation, that the hedging strategy of the corresponding contingent claim is given by \(\frac {\partial C}{\partial S}\) shares of the stock and investing the remaining money in the money market account in a way that the strategy becomes self financing.

On the other side the Black-Scholes formula itself indicates how to hedge a European call :

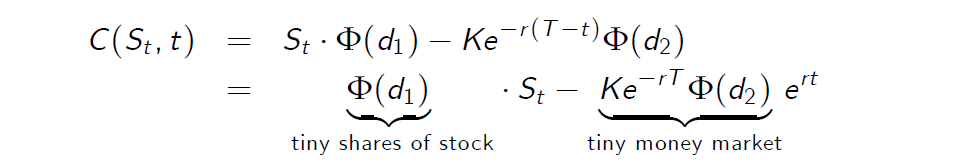
It follows from this consideration as well, that \(\Delta = \Phi(d_1)\).

Greeks : Intuition

1. \(\Delta\) is always positive : An increase in the asset price increases the likely payoff and therefore the price of the option.
2. \(\Phi\) is always positive : An increase in the interest rate is equivalent to lowering the strike price K ( the present price of this future payment decreases with an increase of the interest rate ). This again makes payoff more likely which in e¤ect increases the price of the option.
3. \(\Theta\) is always negative : The option price is decreasing in time, given that everything else is fixed. This fact can be deduced from a no arbitrage argument.
4. vega is always positive : This can be understood by considering that an increase in volatility leads to a wider spread of asset prices

However the payo¤ from a European call option is bounded from below, so that this spread has a more positive effect then a negative effect and is therefore increasing the payoff. The increase in payoff leads to an increase of the price of the option.

Implied Volatility

• We will now study the application of the Greek vega for the computation of implied volatilities.
• First of all : What is an implied volatility?
• Let us consider a European call option.
  • When we set up our Black Scholes model in order to price options, we need to specify some parameters, in fact r and s.
  • r , the interest rate is observable.
• But how to determine the volatility \(\sigma\) that relates to the prices observed at the market.

There are various ways to do this, one is the following : Let us for example observe the price \(C^{obs} (t)\) of a European call option with expiry T and strike K at time t at the market and solve the equation

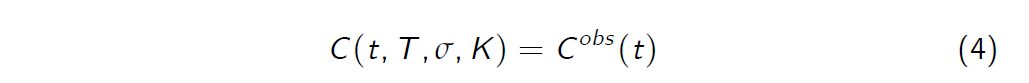
for \(\sigma\).

The vega of the option is given by

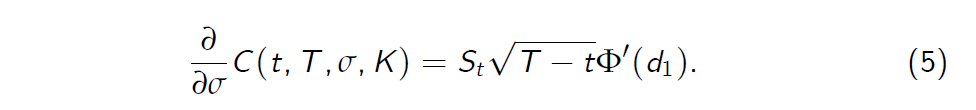
Expression (5) is always strictly positive and therefore Equation (4) has at most one solution for \(\sigma\).

It can be shown, that there exists a solution whenever \(C^{obs} (t)\) is contained in the open interval \(((S_t - Ke^{-r (T-t )})^+, S_t )\).

The solution of equation (4) is called an implied volatility and is denoted \(\sigma_{impl}\) .
How to compute the implied volatility in our case ?
The positivity of expression (4) tells us in particular that the function \(C(t,T, s,K) - C^{obs} (t)\) is strictly increasing as a function of s.
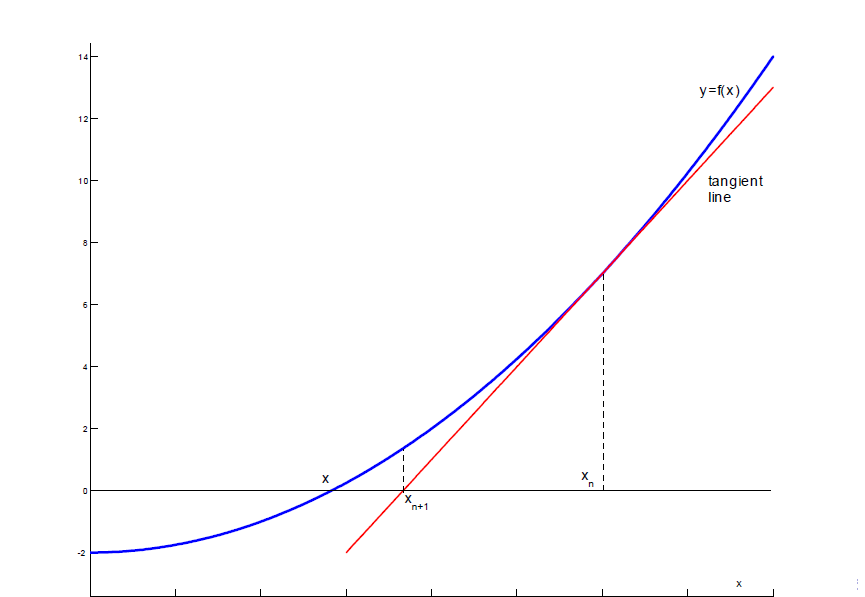
We can therefore compute its zeros numerically by applying the Newton method.
This means that we define an iterative sequence \(\sigma_k\) starting with \(\sigma_0 > 0\) some positive value and

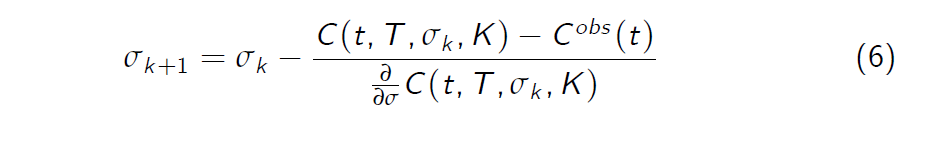
Implied Volatility

This scheme will converge to the solution equation (4) and hence to the implied volatility which re‡ects the observed market price.

Implied Volatility

• The computation of implied volatilities from real market data shows one of the dilemmas of the Black-Scholes model.
• Implied volatilities from di¤erent options lead in general to different results.
• The Black-Scholes model however is based on only one volatility, the volatility which drives the stock prices.
• Systematically one can plot the implied volatilities against strike prices of European call options and time to maturities. One then obtains what is known as the volatility smile.
• The volatility smile is a clear indication that the Black-Scholes model is wrong!

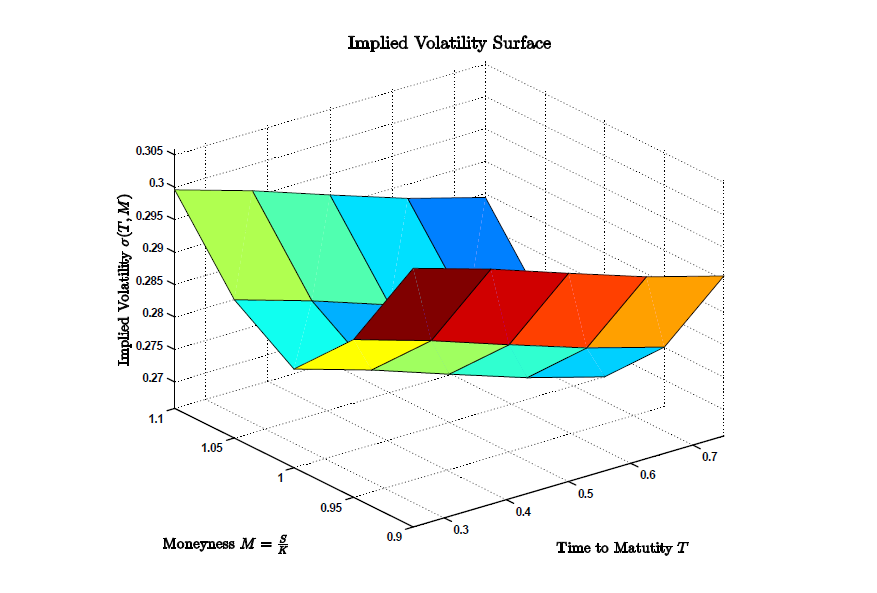
• one can cure some of these problems by using either local volatility models ( nowadays quite famous among financial institutions ) or stochastic volatility models ( for example the Heston model ).
• to set up local volatility models efficient computation of the vega in order to run algorithm (6) is necessary
• for the case of a European call option, luckily closed form solutions for the vega’s are available and one should obviously use them
• but how about options, where we don’t have closed form solution ? Then we have to rely on Monte Carlo methods or other numerical techniques.